Widerstandsthermometer Pt100 sind präzise Temperatursensoren, die in einer Vielzahl von industriellen und wissenschaftlichen Anwendungen weit verbreitet sind. Ihr Prinzip beruht auf der Variation des elektrischen Widerstands eines Platin-Drahts in Abhängigkeit von der Temperatur. Das „Pt“ in Pt100 steht für Platin, das Material, aus dem der Draht besteht, und die „100“ gibt an, dass der Widerstand bei 0°C genau 100 Ohm beträgt.
Pt100-Widerstandsthermometer bieten einen breiten Temperaturbereich, der von -200°C bis +850°C reicht, und zeichnen sich durch ihre hohe Genauigkeit aus. Ihre Widerstand-Temperatur-Kurve ist nahezu linear, was die Kalibrierung und Interpretation der gemessenen Werte erleichtert.
Diese Sensoren verändern ihren elektrischen Widerstand proportional zur Temperaturänderung. Der Temperaturkoeffizient beträgt etwa 0,385 Ohm/°C bei 0°C. Pt100-Sensoren verfügen in der Regel über zwei, drei oder vier Anschlüsse. Dem entsprechend können sie in verschiedenen Schaltungskonfigurationen verwendet werden, darunter 2-Leiter-, 3-Leiter- und 4-Leiter-Schaltung.
Um genaue Messungen sicherzustellen, müssen Pt100-Widerstandsthermometer vor äußeren Einflüssen wie Feuchtigkeit und mechanischer Belastung geschützt werden. Dies geschieht oft durch den Einsatz von Schutzrohren. Zusätzlich sollten sie regelmäßig kalibriert werden, entweder in spezialisierten Laboren oder mithilfe von Referenzthermometern.
Pt100-Sensoren finden in zahlreichen Anwendungen Verwendung, darunter die Lebensmittelindustrie, Labors, Klimatisierungstechnik, die Automobilindustrie und die chemische Verfahrenstechnik.
Inhalt
Wie funktionieren Widerstandsthermometer?
Widerstandsthermometer werden häufig für präzise Temperaturmessungen eingesetzt. Der übliche Temperaturbereich liegt zwischen etwa -50 °C und 600 °C, obwohl Spezialanwendungen existieren, bei denen Widerstandsthermometer von -200 °C bis über 1000 °C eingesetzt werden. Das abgebildete Pt100 Widerstandsthermometer stammt aus dem Kalibrierlabor der Firma Klasmeier.
Das Messprinzip dieser Thermometer basiert auf der Messung des elektrischen Widerstands von Messwiderständen, wofür das Ohmsche Gesetz grundlegend ist:
U = R ⋅ I = Konstante
wobei:
U = Spannung,
R = Widerstand,
I = Strom
Im Schulunterricht wird das Ohmsche Gesetz oft als Dreieck dargestellt, das den Zusammenhang zwischen Strom, Spannung und Widerstand verdeutlicht.
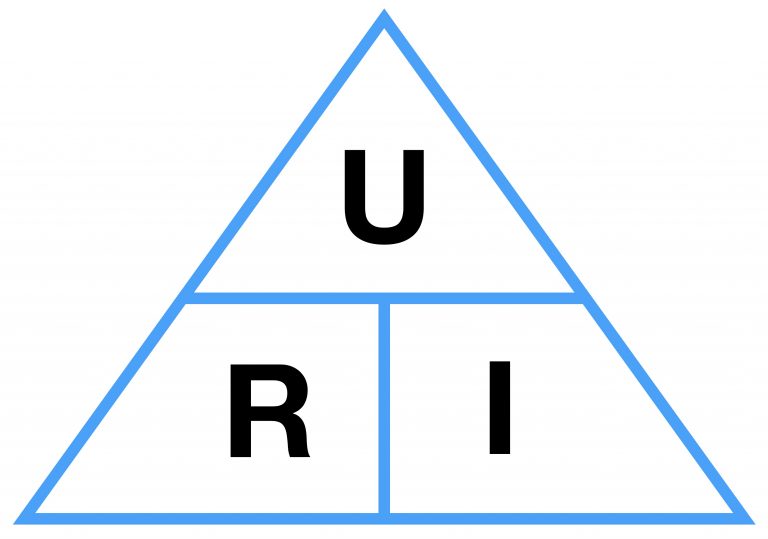
Wenn zwei dieser Größen bekannt sind, kann die dritte berechnet werden. Im Schaltplan wird das Ohmsche Gesetz wie in der folgenden Grafik dargestellt.
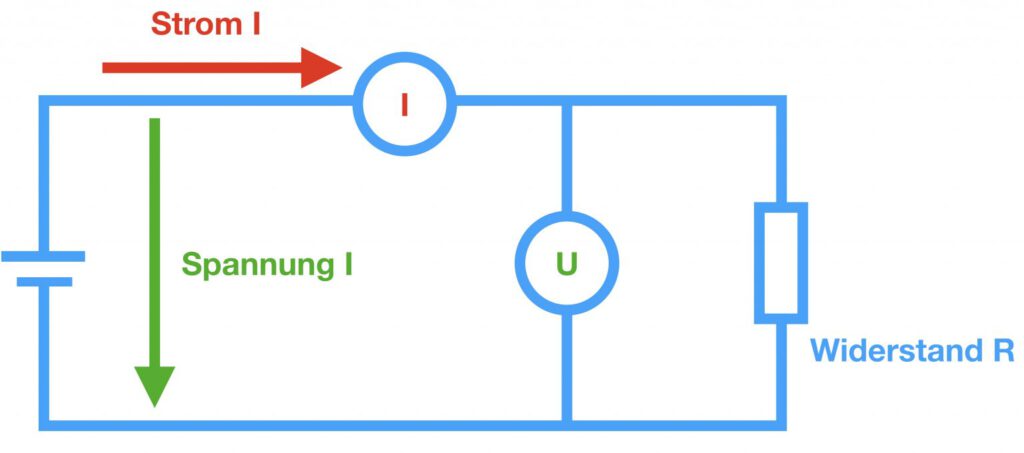
Die Zusammenhänge der Widerstandsmessung und somit der Widerstandsthermometer können auch grafisch in einem Schaubild dargestellt werden.
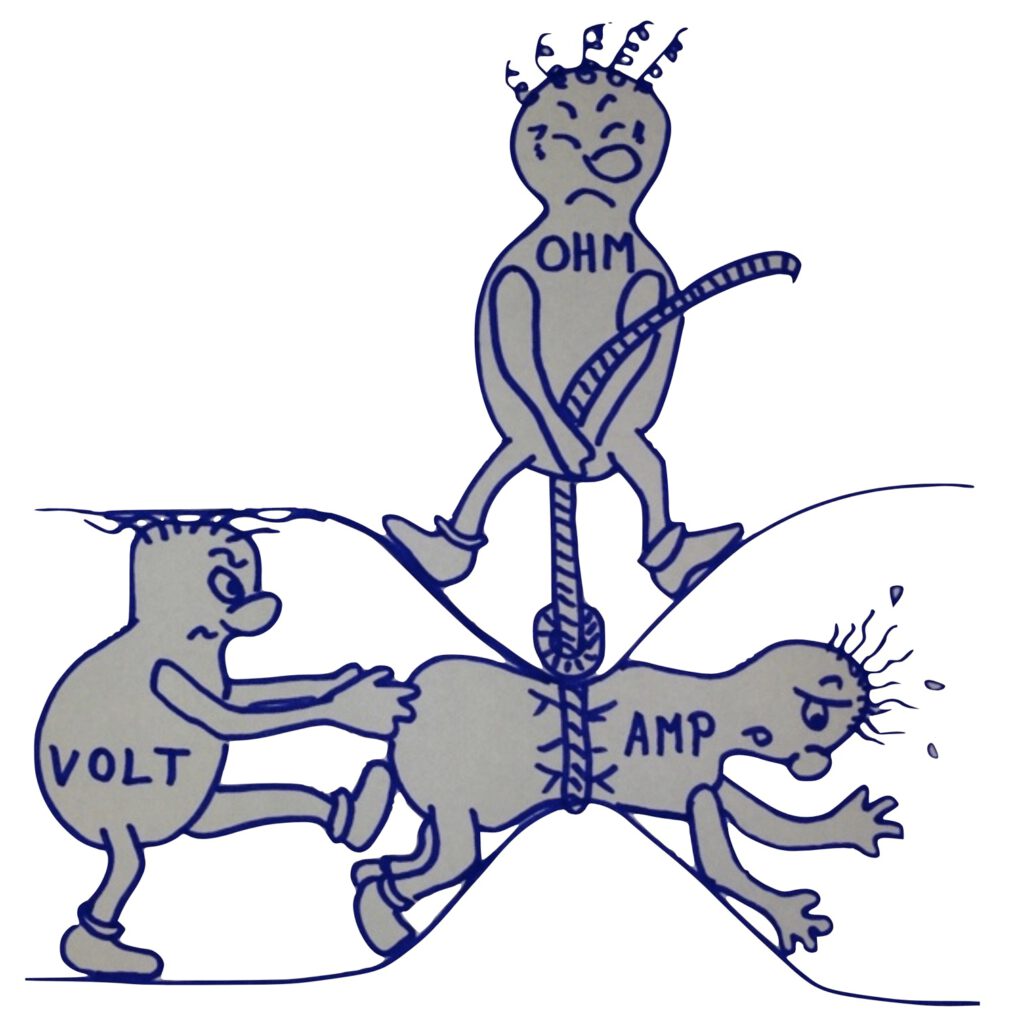
Hierbei wird das „VOLT-Männchen“ (U – Spannung) vom „AMP-Männchen“ (I – Strom) durch ein Rohr gedrückt, während das „OHM-Männchen“ (R – Widerstand) versucht, dies zu verhindern, indem es das Rohr verengt. Der Erfolg des „OHM-Männchens“ ist temperaturabhängig: Je wärmer es ist, desto schwerer wird es für das „VOLT-Männchen“, das „AMP-Männchen“ zu bewegen. Da diese temperaturabhängige Wirkung reproduzierbar ist, kann das Prinzip der elektrischen Widerstandsmessung zur Temperaturmessung genutzt werden. Ein gemessener Widerstand R in Ohm wird über eine bekannte Beziehung in eine Temperatur T in °C oder K umgerechnet.
Prinzipiell kann jeder elektrische Leiter, für den das Ohmsche Gesetz gilt, als Thermometer verwendet werden. Der spezifische Widerstand ist die physikalische Konstante, die diese Eigenschaft beschreibt. Eine Übersicht in zeigt die verschiedenen spezifischen Widerstände von Materialien bei 20 °C.
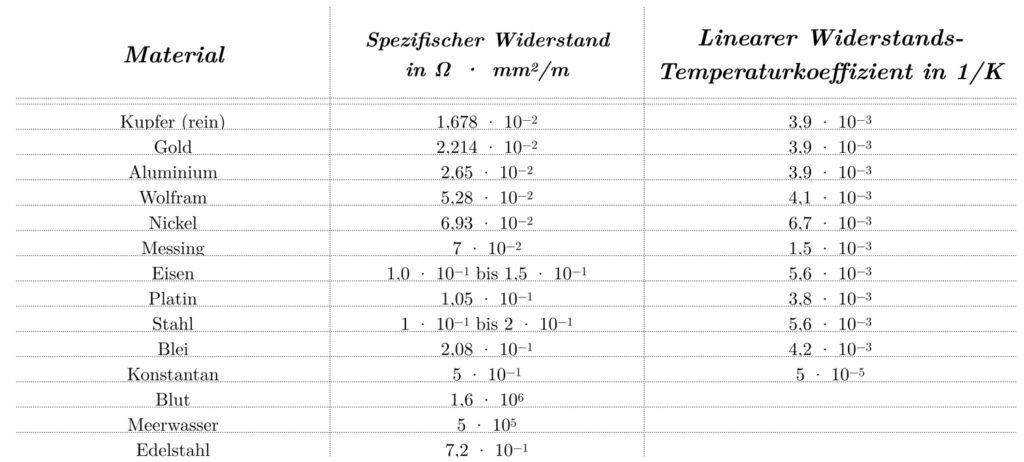
Obwohl alle genannten Materialien grundsätzlich zur Temperaturmessung verwendet werden können, gibt es bestimmte Auswahlkriterien für die Materialauswahl von Thermometern. Das Material sollte einen hohen spezifischen Widerstand aufweisen und grundsätzlich geeignet sein. Zum Beispiel hat menschliches Blut mit 1,6×106 Ω⋅mm2 /m einen ausgezeichneten spezifischen Widerstand, ist jedoch nicht für die industrielle Herstellung von Thermometern geeignet. Metalle sind für diesen Zweck besser geeignet.
Neben dem spezifischen Widerstand ist auch der lineare Widerstand-Temperaturkoeffizient wichtig. Dieser beschreibt die Änderung des Widerstands eines Materials pro Grad Celsius und wird in 1/K angegeben. Er kann auch als Empfindlichkeit bezeichnet werden. Um die Anforderungen an die Messtechnik zu minimieren, sollte dieser Koeffizient möglichst groß sein. Es gilt also, den besten Kompromiss zwischen Kosten, grundsätzlicher Eignung des Materials, spezifischem Widerstand und Widerstands-Temperaturkoeffizienten zu finden.
Nickel und Platin haben sich als geeignete Materialien herausgestellt. Anfangs galten Nickel-Messwiderstände, wie z.B. Ni100, als Favoriten, da sie eine höhere Empfindlichkeit als Platin-Messwiderstände aufwiesen. Allerdings zeigten sie höhere Grenzabweichungen und einen begrenzten Temperaturbereich. Die Norm für Nickel-Thermometer, DIN 43760, wurde in den 1990er Jahren zurückgezogen. Seitdem werden Nickel-Messwiderstände hauptsächlich in technischen Sonderanwendungen eingesetzt.
Mit der Zeit haben sich Platin-Messwiderstände, wie z.B. Pt100, durchgesetzt. Sie sind in der industriellen Messtechnik weit verbreitet und stellen heute den Standard der elektrischen Temperaturmessung mit Widerstandsthermometern dar.
Die Pt100-Kennlinie für Widerstandsthermometer einfach erklärt
Platin-Sensoren haben sich als Widerstandsthermometer etabliert. Der Zusammenhang zwischen der Temperatur und dem Widerstand bei Platin-Thermometern wird nicht proportional, sondern mit einem Polynom höherer Ordnung beschrieben:
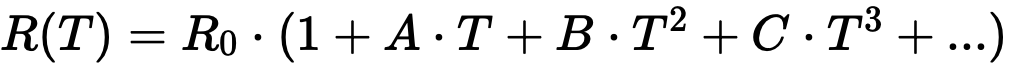
Hierbei bedeuten:
R(T) = Widerstand des Thermometers
R0 = Widerstand des Thermometers bei 0 °C
A, B, C, … = Individuelle Parameter des Thermometers oder Norm
T = Temperatur
Callendar-Van Dusen Gleichung
Die Callendar-Van Dusen Gleichung ist eine Formel, die verwendet wird, um diesen Zusammenhang zwischen der Temperatur und dem elektrischen Widerstand eines Platin-Widerstandstemperaturfühlers zu beschreiben.
Die Callendar-Van-Dusen-Gleichung wird abgekürzt auch als „CVD“ bezeichnet und wird bereits seit den 1920er Jahren angewendet. Die Kennlinie ist in der DIN EN 60751 genormt, die industrielle Platin-Widerstandsthermometer und Platin-Temperatursensoren beschreibt. Sie wurde erstmals in den 1990ern veröffentlicht und ist in ihrer letzten Überarbeitung als DIN EN 60751:2009-05 immer noch gültig.
Die Callendar-Van-Dusen-Gleichung selbst kann in zwei Teilen formuliert werden, für Temperaturen über und unter 0 °C:
Für Temperaturen T > 0 °C:
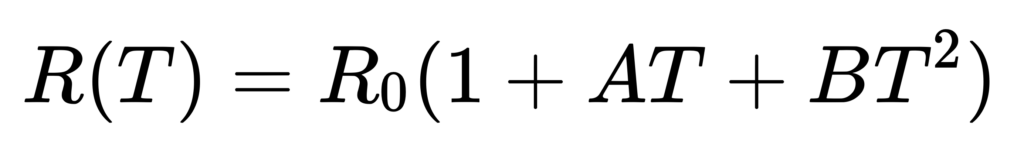
Für Temperaturen T < 0 °C:
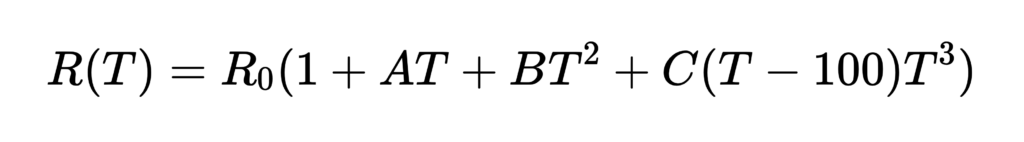
Hierbei ist:
- R(T) der Widerstand bei der Temperatur ( T )
- R0 der Widerstand bei 0 °C
- A, B, und C sind Koeffizienten, die vom Platin-Widerstandsthermometer abhängig sind
In der DIN EN 60751:2009-05 sind die Koeffizienten für die Callendar-Van-Dusen-Gleichung genormt:
A=3,9083×10 −3 °C-1
B=−5,775×10 −7 °C-2
C=−4,183×10 −12 °C-4
Es ist aber auch möglich, einzelne Thermometer zu kalibrieren und individuelle Koeffizienten zu berechnen. Dies hat den Vorteil, dass das Thermometer nicht mehr anhand der Grenzabweichungen der Norm beurteilt werden muss, sondern individuell an seine eigene Kennlinie angepasst werden kann.
Die Callendar-Van-Dusen-Gleichung ermöglicht es, sehr präzise Temperaturmessungen durchzuführen, indem man den gemessenen Widerstand des Thermometers in die Callendar-Van-Dusen-Gleichung einsetzt und die Temperatur berechnet.
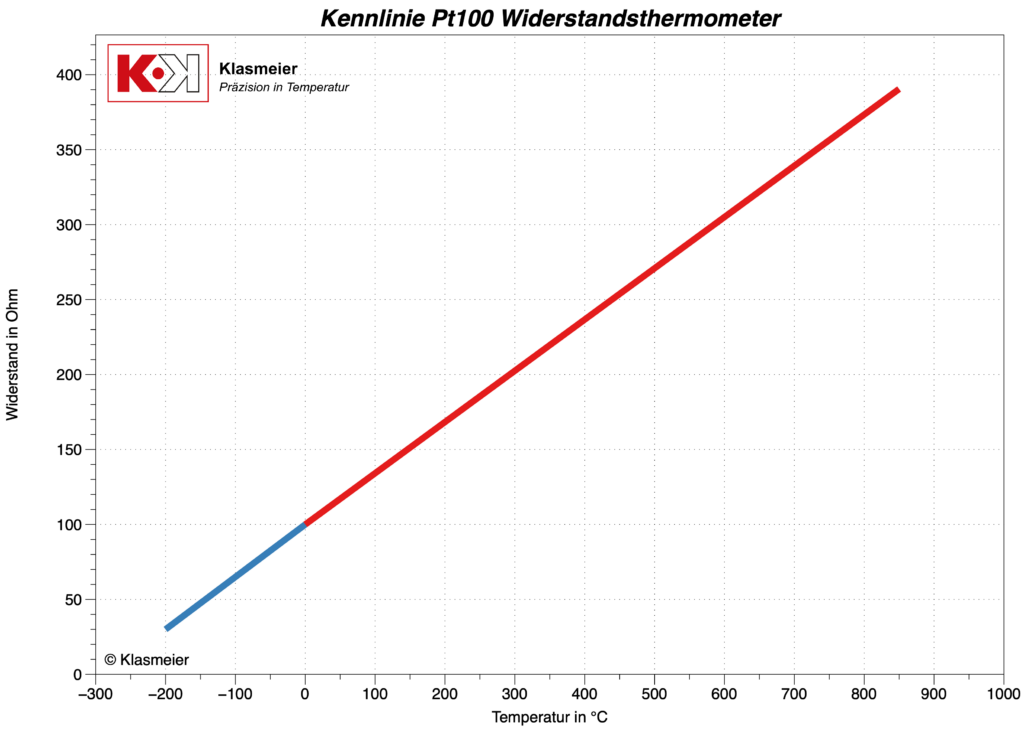
Die folgende Grafik zeigt die zwei Temperaturbereiche der Callendar-Van-Dusen-Gleichung. Blau dargestellt ist der Temperaturbereich von -200 °C bis 0 °C und der Temperaturbereich von 0 °C bis 850 °C ist Rot dargestellt.
Der Nennwiderstand R0 von Widerstandsthermometern
Um die Messwiderstände besser zu klassifizieren, wurde in der Norm DIN EN 60751 der sogenannte Nennwiderstand R0 eingeführt. Dieser beschreibt den elektrischen Widerstand des Temperatursensors bei 0 °C. Zum Beispiel hat ein Pt100-Temperatursensor bei 0 °C einen Widerstand von 100 Ohm. In der Norm werden folgende Nennwiderstände aufgeführt:
- Pt 10 = 10 Ohm bei 0 °C
- Pt 100 = 100 Ohm bei 0 °C
- Pt 500 = 500 Ohm bei 0 °C
- Pt 1.000 = 1.000 Ohm bei 0 °C
Abweichende Nennwiderstände wie Pt 25, Pt 2,5 oder Pt 0,25 werden bei Präzisions-Thermometern verwendet und erfüllen oft die Anforderungen der ITS-90. Diese werden dann als SPRT oder Normal-Thermometer bezeichnet. Bei Laboranwendungen werden Pt 25-Thermometer oft bevorzugt, da sie einen guten Kompromiss zwischen Stabilität, Empfindlichkeit und Eigenerwärmung bieten.
Temperaturkoeffizient bei Widerstandsthermometern
Der Unterschied zwischen genormten Thermometern und Normal-Thermometern gemäß der ITS-90 zeigt sich im sogenannten Temperaturkoeffizienten, der in der Norm durch eine Widerstandsmessung bei 0 °C und 100 °C definiert ist:
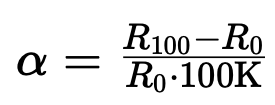
Hierbei bedeuten:
alpha = Steigerung des Thermometers in 1/K
R100 = Widerstand bei 100 °C in Ohm
R0 = Widerstand bei 0 °C in Ohm
Der Alpha-Wert von industriellen Temperatursensoren nach Norm beträgt 3,85 10^-3/K, während der Alpha-Wert bei Normal-Thermometern gemäß ITS-90 bei 3,92875 10^-3/K liegt. Dieser Wert entspricht der Empfindlichkeit von spektralreinem Platin in diesem Temperaturbereich.
Empfindlichkeit bei Widerstandsthermometern
Die Empfindlichkeit eines Widerstandsthermometers beschreibt, wie stark sich der Widerstand des Sensors in Bezug auf eine Temperaturänderung ändert. Sie ist ein Maß dafür, wie genau der Sensor auf Temperaturänderungen reagiert. Beim Pt100 ändert sich der Widerstand um etwa 0,385 Ohm für jeden Grad Celsius Temperaturänderung. Diese Änderungsrate, bekannt als der Temperaturkoeffizient, ist ein direktes Maß für die Empfindlichkeit des Sensors. Die Empfindlichkeit ist entscheidend für die Genauigkeit und Auflösung des Sensors. Ein Sensor mit höherer Empfindlichkeit kann kleinere Temperaturänderungen erkennen und ermöglicht genauere Temperaturmessungen. Dies ist besonders wichtig in Anwendungen, wo präzise Temperaturkontrolle erforderlich ist, wie in Laboren oder in der Prozesssteuerung in der Industrie.
Es ist jedoch auch zu beachten, dass Temperatursensoren mit einer großen Empfindlichkeit oft eine hohe Eigenerwärmung besitzen und sich weniger langzeitstabil verhalten. Deswegen muß das Verhältnis zwischen Nennwert und Empfindlichkeit eines Temperatursensors sehr bedacht gewählt werden.
Um einen definierten Nennwiderstand zu erreichen, wird die Länge oder der Durchmesser des Platin-Drahts im Messwiderstand angepasst. Dadurch ändert sich nicht nur der Widerstand, sondern auch die Empfindlichkeit der Sensoren auf ca:
- Pt 10 = 0,04 Ohm / K
- Pt 100 = 0,4 Ohm / K
- Pt 500 = 2 Ohm / K
- Pt 1.000 = 4 Ohm / K
Anschlusstechnologien von Widerstandsthermometern
Widerstandsthermometer können mit Messgeräten, Datenloggern oder Messbrücken verbunden werden, und dafür gibt es verschiedene Techniken.
- Zwei-Leiter-Technik
- Drei-Leiter-Technik
- Vier-Leiter-Technik
Zwei-Leiter-Technik
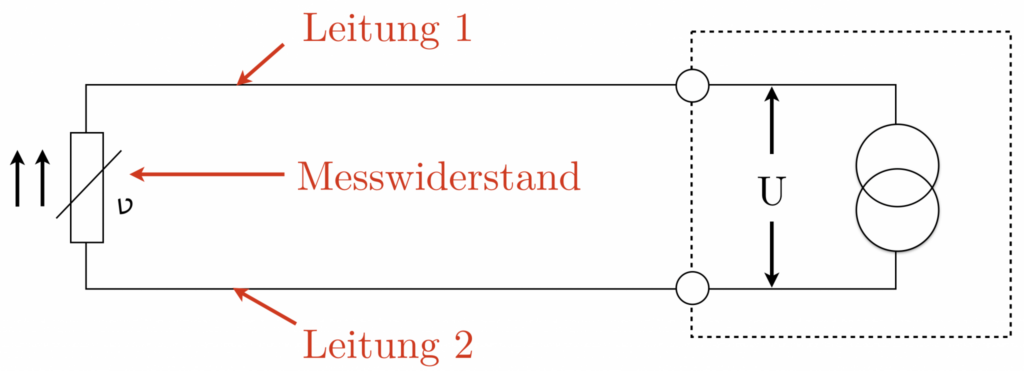
Die Zwei-Leiter-Technik zeigt, wie man einen Temperatursensor mit einem Messgerät verbindet, wie es auf dem Bild zu sehen ist. Dabei ist wichtig, dass der Widerstand der Verbindungskabel berücksichtigt wird, weil er mit dem Messwiderstand in Reihe geschaltet ist.
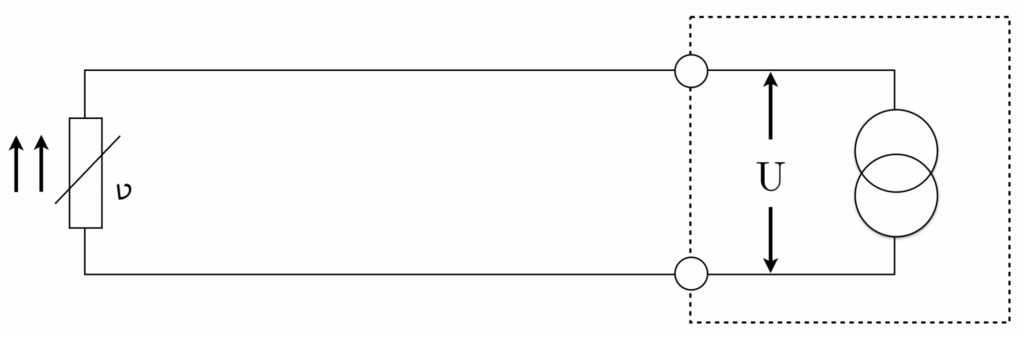
Die resultierende Messung ergibt sich aus der Summation des Widerstands von Leitung 1, dem Messwiderstand (dem eigentlichen Temperatursensor) und Leitung 2, was zu einer erhöhten Messung führt. Daher ist eine Korrektur des Messergebnisses unabdingbar, um Messfehler zu eliminieren.
Ein exemplarisches Berechnungsbeispiel demonstriert das Ausmaß der Messabweichung unter bestimmten Anwendungsbedingungen. Angenommen, ein Temperatursensor wird mittels einer Kupferleitung verbunden, unter den folgenden spezifizierten Bedingungen:
- Spezifischer Widerstand der Kupferleitung bei Raumtemperatur: 0,017
- Querschnitt der Leitung: 0,5 mm^2
- Länge der Leitung: ca. 50 m
Die Messabweichung aufgrund der Anschlussleitung kann mittels der Gleichung
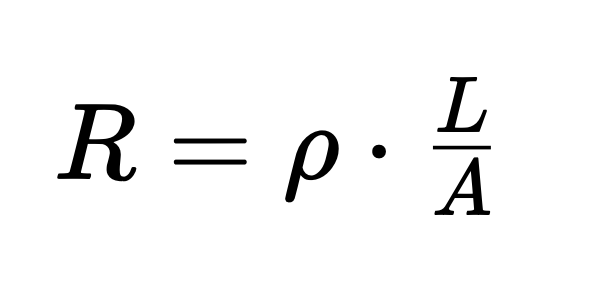
ermittelt werden, wobei:
- R den Leiterwiderstand,
- \rho den spezifischen Widerstand,
- L die Leiterlänge und
- A die Fläche des Querschnitts repräsentiert.
In diesem Kontext resultiert ein Leiterwiderstand von 3,4 Ohm:
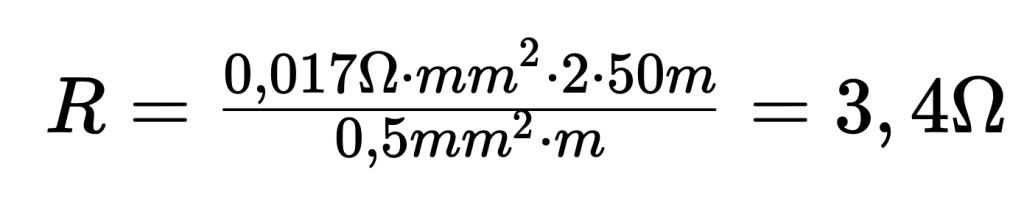
Unter Berücksichtigung einer Sensitivität ( E ) eines PT 100 Temperatursensors von ca. 0,385 Ohm / K, ergibt sich eine Messabweichung von 8,8 K.
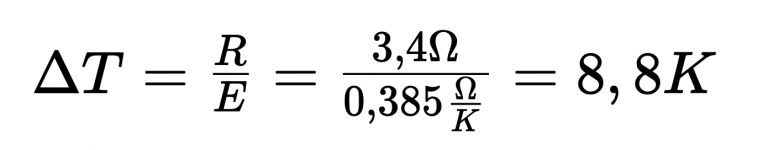
Die Leitungslänge von ca. 50 m ist für den „Hinweg“ (Leitung 1) als auch für den „Rückweg“ (Leitung 2) zweimal zu berücksichtigen.
Historisch gesehen war es durchaus konventionell, Thermometer in Produktionsanlagen mittels der Zwei-Leiter-Technik zu verbinden. Vor der Ära digitaler Technologie, welche die Korrektur systematischer Fehler vereinfacht, wurden Korrekturtabellen genutzt, um akkurate Messwerte zu erzielen.
Ein Beispiel illustriert Korrekturwerte einer10 m langen Anschlussleitung in Abhängigkeit vom Leitungsquerschnitt.
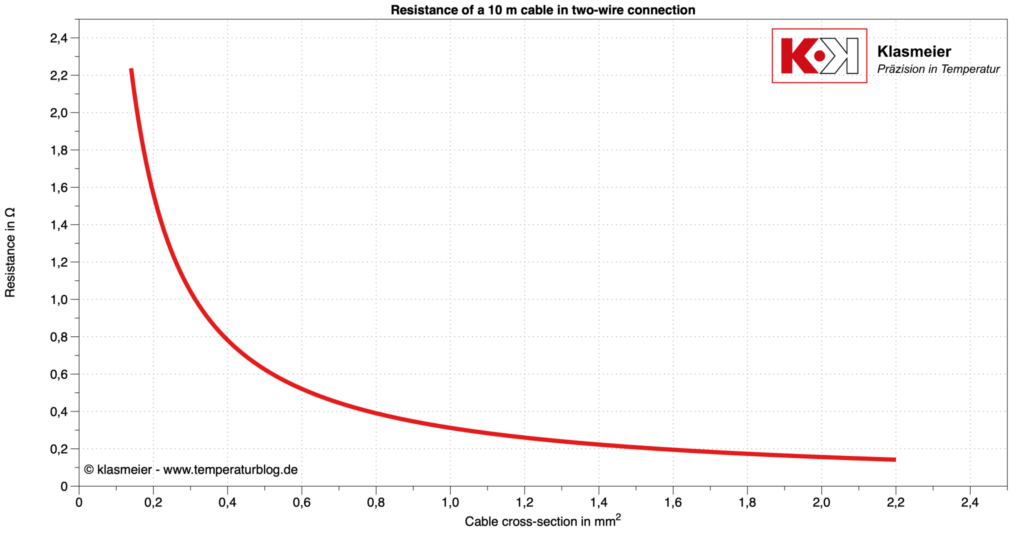
Bei einer Anschlussleitung mit einem Leitungsquerschnitt von 0,5 mm^2 beträgt der Widerstand in einer 10 m langen Zwei-Leiter-Schaltung 0,6 Ohm. Dies impliziert, dass die Messwerte um diesen Faktor korrigiert werden müssen. Bei einem Pt100 entspricht dies etwa 1,6 °C.
In der nachfolgenden Grafik werden die Korrekturwerte für einen Pt100 in Relation zum Querschnitt einer 10 m langen Kupferleitung in der Zwei-Leiter-Technik dargestellt.
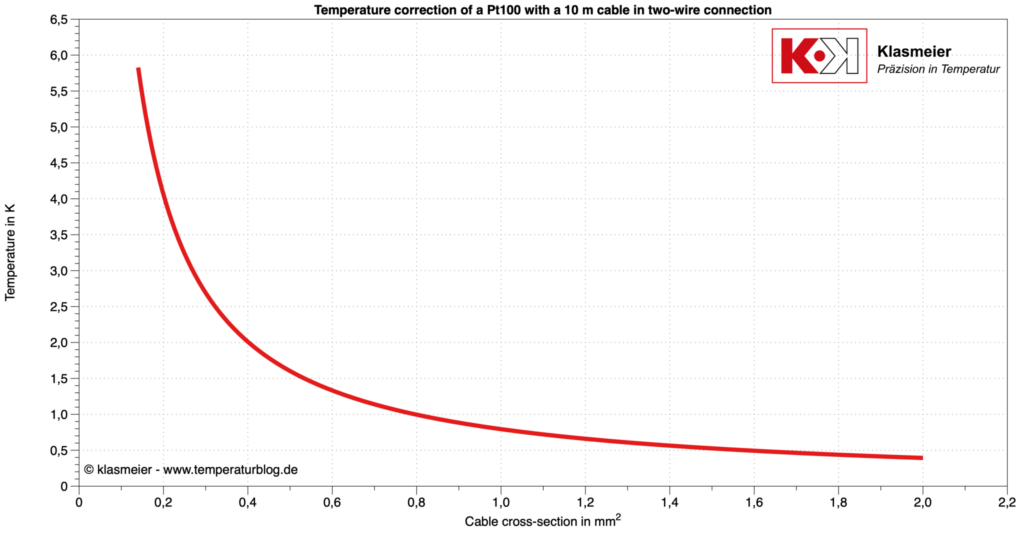
Drei-Leiter-Technik
Die Drei-Leiter-Technik stellt eine Optimierung gegenüber der Zwei-Leiter-Technik dar, insbesondere im Hinblick auf die Minimierung von Messfehlern aufgrund von Leitungswiderständen. In dieser Konfiguration werden drei Leitungen verwendet, wobei zwei Leitungen parallel zum Messwiderstand und eine dritte Leitung zur Kompensation des Leitungswiderstands geschaltet sind.
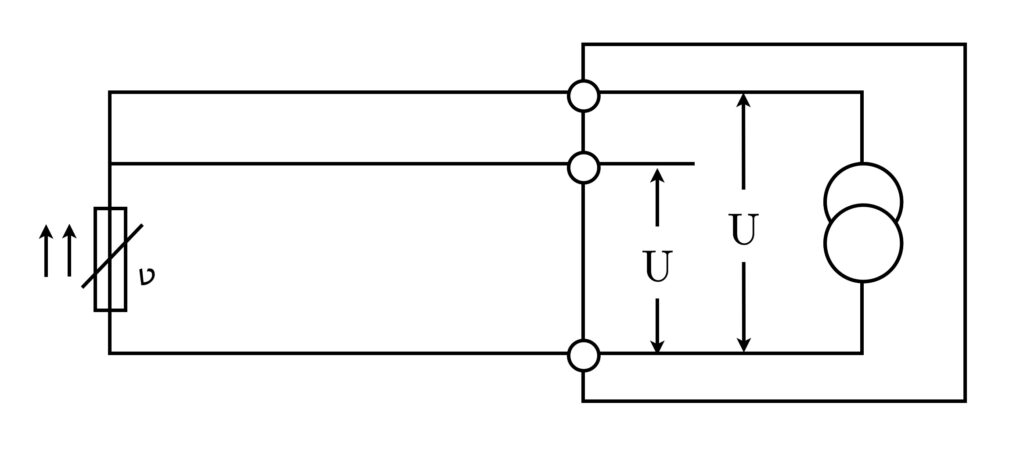
Die Kompensation des Leitungswiderstands erfolgt durch die Messbrücke, welche den Widerstand der dritten Leitung berücksichtigt und somit den Gesamtwiderstand der Anschlussleitungen subtrahiert. Dies resultiert in einer präziseren Messung des eigentlichen Messwiderstands, da die Einflüsse der Anschlussleitungen minimiert werden.
Obwohl die Drei-Leiter-Technik eine signifikante Verbesserung gegenüber der Zwei-Leiter-Technik darstellt, ist sie dennoch anfällig für Fehler aufgrund von Temperaturänderungen und unterschiedlichen Leitungslängen, welche die Kompensation des Leitungswiderstands beeinträchtigen können.
Vier-Leiter-Technik
Die Vier-Leiter-Technik, auch als Kelvin-Vierleiter-Messung bekannt, repräsentiert eine weitere Optimierung in der Präzision der Widerstandsmessung, insbesondere für Anwendungen, bei denen höchste Genauigkeit erforderlich ist. Diese Technik verwendet zwei zusätzliche Leitungen, um den Messstrom zu liefern und den Spannungsabfall über dem Sensor zu messen, wodurch der Einfluss des Leitungswiderstands eliminiert wird.
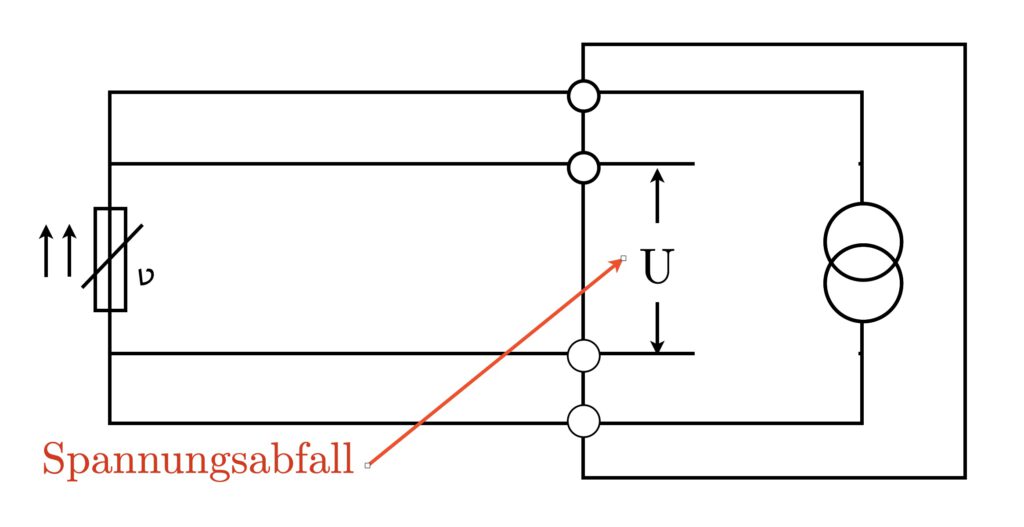
In dieser Konfiguration fließt der Messstrom durch zwei der Leitungen (Stromleitungen), während die anderen zwei Leitungen (Spannungsleitungen) dazu dienen, den Spannungsabfall direkt über dem Sensor zu messen. Da der Messstrom nicht durch die Spannungsleitungen fließt, wird der Leitungswiderstand dieser Leitungen nicht in die Messung einbezogen, was zu einer höheren Messgenauigkeit führt.
Die Vier-Leiter-Technik ist insbesondere für Anwendungen mit niedrigen Widerstandswerten und langen Leitungslängen von Vorteil, da sie eine präzise Messung ermöglicht, die frei von den Einflüssen der Leitungswiderstände ist.
Zusammenfassend bieten die Drei- und Vier-Leiter-Techniken verbesserte Genauigkeit und Zuverlässigkeit im Vergleich zur Zwei-Leiter-Technik, indem sie den Einfluss von Leitungswiderständen minimieren oder eliminieren. Die Wahl der geeigneten Technik hängt von den spezifischen Anforderungen der Anwendung, wie Messgenauigkeit, Umgebungsbedingungen und wirtschaftlichen Überlegungen, ab.
Quellen
- Frank Bernhard: Handbuch der Technischen Temperaturmessung, 2. Auflage
- Thomas Klasmeier: Tabellenbuch „Temperatur“, Ausgabe 3
- Industrielle Platin-Widerstandsthermometer und Platin-Temperatursensoren (IEC 60751:2022)
- ISOTECH Kupferpunkt-Thermometer Nr. 108462 bis fast 1100°C.
- Spezifischer Widerstand
- DIN 43760
- Ohmsche Gesetz
