Los termómetros de resistencia Pt100 son sensores de temperatura precisos que se utilizan ampliamente en una variedad de aplicaciones industriales y científicas. Su principio se basa en la variación de la resistencia eléctrica de un hilo de platino en función de la temperatura. El «Pt» en Pt100 significa platino, el material del que está hecho el cable, y el «100» indica que la resistencia a 0°C es exactamente de 100 ohmios.
Las termorresistencias Pt100 ofrecen un amplio rango de temperatura de -200 °C a +850 °C y se caracterizan por su alta precisión. Su curva resistencia-temperatura es casi lineal, lo que facilita la calibración e interpretación de los valores medidos.
Estos sensores cambian su resistencia eléctrica en proporción al cambio de temperatura. El coeficiente de temperatura es de aproximadamente 0,385 ohmios/°C a 0°C. Los sensores Pt100 suelen tener dos, tres o cuatro conexiones. En consecuencia, se pueden utilizar en diversas configuraciones de circuitos, incluidos circuitos de 2, 3 y 4 cables.
Para garantizar mediciones precisas, las termorresistencias Pt100 deben protegerse de influencias externas como la humedad y las tensiones mecánicas. Esto se suele hacer mediante el uso de tubos protectores. Además, conviene calibrarlos periódicamente, ya sea en laboratorios especializados o utilizando termómetros de referencia.
Los sensores Pt100 se utilizan en numerosas aplicaciones, incluida la industria alimentaria, laboratorios, aire acondicionado, automoción e ingeniería química.
Contenido
¿Cómo funcionan los termómetros de resistencia?
Los termómetros de resistencia se utilizan a menudo para mediciones precisas de temperatura. El rango de temperatura habitual está entre aproximadamente -50 °C y 600 °C, aunque existen aplicaciones especializadas que utilizan termómetros de resistencia de -200 °C a más de 1000 °C. La termorresistencia Pt100 mostrada procede del laboratorio de calibración Klasmeier.
El principio de medición de estos termómetros se basa en la medición de la resistencia eléctrica de resistencias de medición, para lo cual la ley de Ohm es fundamental:
U = R ⋅ I = constante
dónde:
U = voltaje,
R = resistencia,
yo = actual
En las lecciones escolares, la ley de Ohm suele representarse como un triángulo que ilustra la relación entre corriente, voltaje y resistencia.
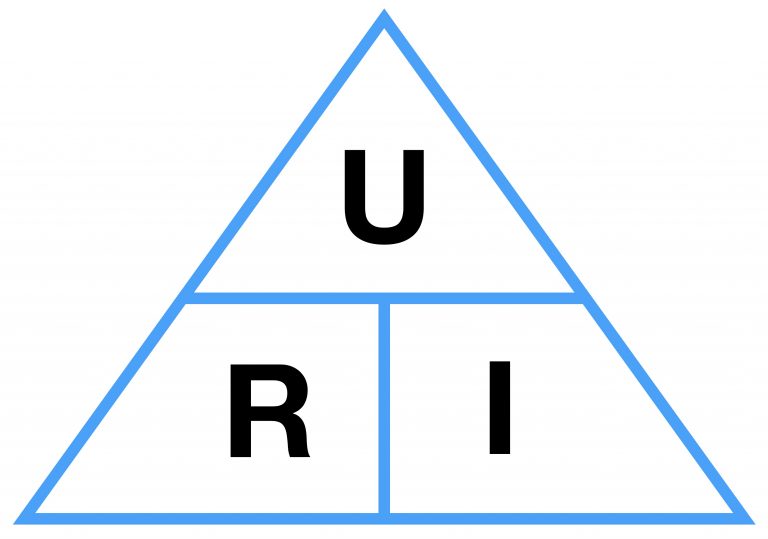
Si se conocen dos de estas cantidades, se puede calcular la tercera. En el diagrama del circuito, la ley de Ohm se muestra como en el siguiente gráfico.
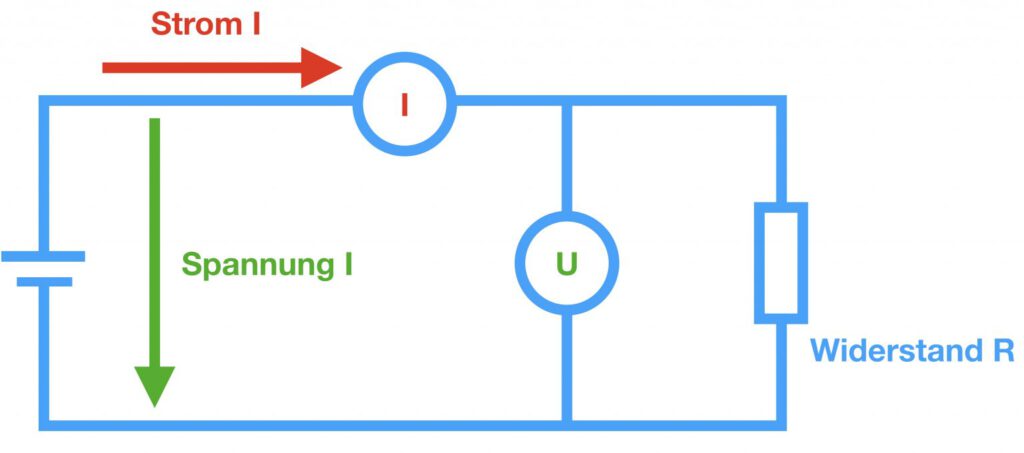
Las relaciones entre la medición de resistencia y, por tanto, las termorresistencias también se pueden representar gráficamente en un diagrama.
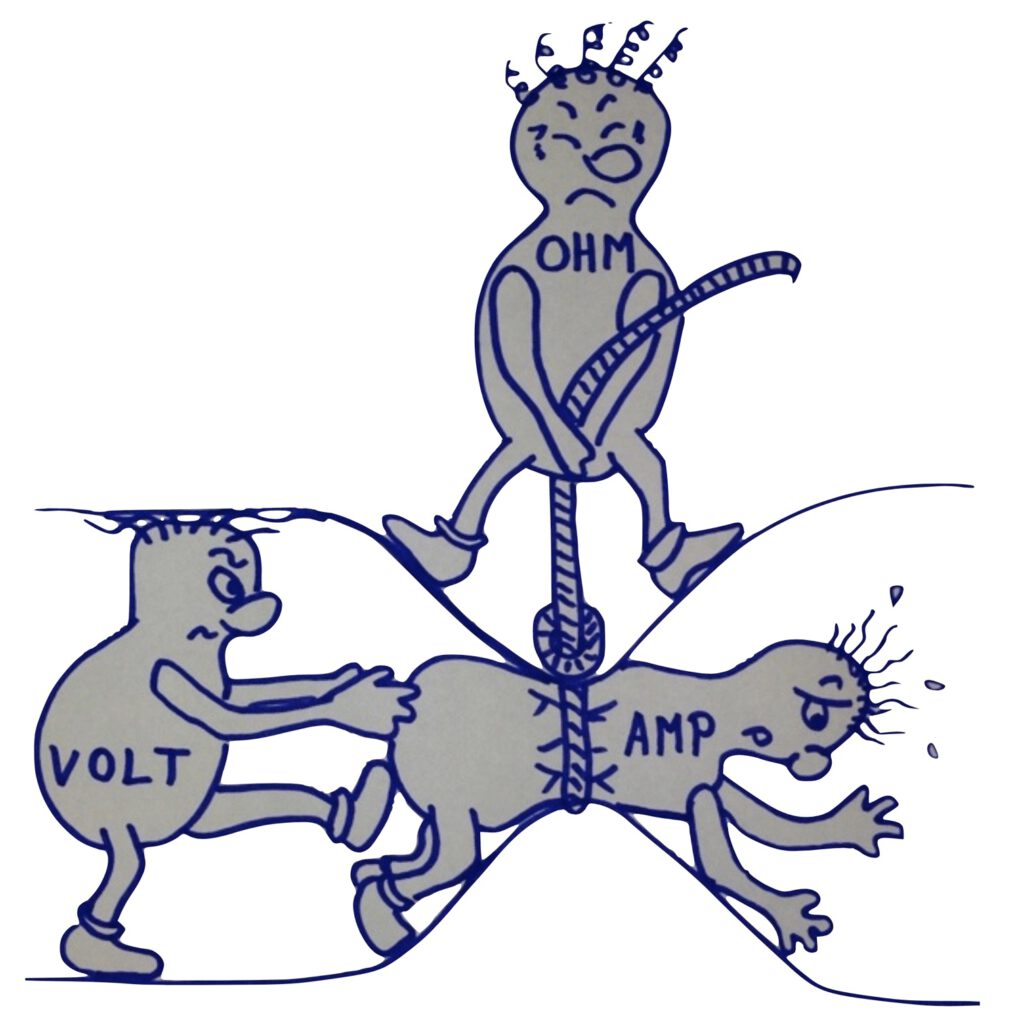
Aquí, el «hombre VOLT» (U – voltaje) es empujado a través de un tubo por el «hombre AMP» (I – corriente), mientras que el «hombre OHM» (R – resistencia) intenta evitarlo estrechando el tubo. El éxito del «macho OHM» depende de la temperatura: cuanto más caliente hace, más difícil le resulta al «macho VOLT» mover al «macho AMP». Dado que este efecto dependiente de la temperatura es reproducible, se puede utilizar el principio de medición de la resistencia eléctrica para medir la temperatura. Una resistencia medida R en ohmios se convierte en una temperatura T en °C o K utilizando una relación conocida.
En principio, cualquier conductor eléctrico al que se aplique la ley de Ohm puede utilizarse como termómetro. La resistencia específica es la constante física que describe esta propiedad. Una descripción general muestra las diferentes resistencias específicas de los materiales a 20 °C.
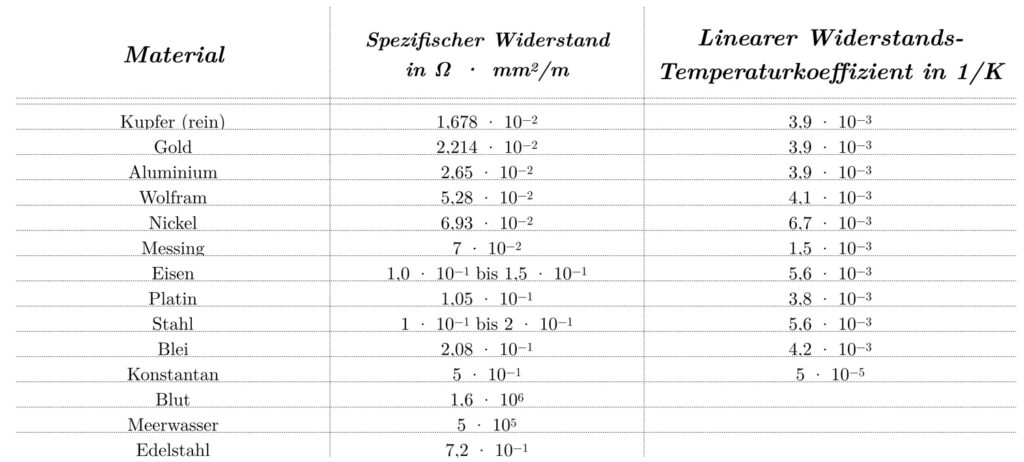
Aunque en principio todos los materiales mencionados pueden utilizarse para medir la temperatura, existen ciertos criterios para la elección del material de los termómetros. El material debe tener una alta resistencia específica y ser fundamentalmente adecuado. Por ejemplo, la sangre humana tiene una resistividad excelente de 1,6×106 Ω⋅mm2 /m, pero no es adecuada para la producción de termómetros industriales. Los metales son más adecuados para este fin.
Además de la resistencia específica, también es importante el coeficiente lineal de resistencia-temperatura. Esto describe el cambio en la resistencia de un material por grado Celsius y se expresa en 1/K. También se le puede llamar sensibilidad. Para minimizar los requisitos de la tecnología de medición, este coeficiente debería ser lo más grande posible. Por tanto, es importante encontrar el mejor compromiso entre costes, idoneidad básica del material, resistencia específica y coeficientes resistencia-temperatura.
Se ha demostrado que el níquel y el platino son materiales adecuados. Al principio, las resistencias de medición de níquel, como por ejemplo Ni100, se consideraban las favoritas porque tenían una mayor sensibilidad que las resistencias de medición de platino. Sin embargo, mostraron desviaciones límite más altas y un rango de temperatura limitado. La norma para los termómetros de níquel, DIN 43760, fue retirada en los años 90. Desde entonces, las resistencias de medición de níquel se utilizan principalmente en aplicaciones técnicas especiales.
Con el tiempo se han ido popularizando las resistencias de medición de platino, como por ejemplo la Pt100. Se utilizan ampliamente en la tecnología de medición industrial y hoy representan el estándar para la medición eléctrica de temperatura con termómetros de resistencia.
La curva característica Pt100 para termorresistencias explicada de forma sencilla
Los sensores de platino se han consolidado como termómetros de resistencia. La relación entre temperatura y resistencia en los termómetros de platino no se describe proporcionalmente, sino con un polinomio de orden superior:
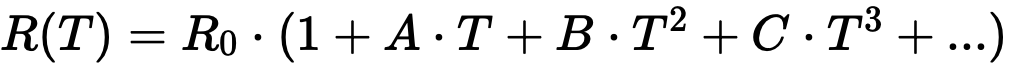
Esto significa:
R(T) = resistencia del termómetro
R0 = resistencia del termómetro a 0 °C
A, B, C, … = Parámetros individuales del termómetro o patrón
T = temperatura

Por tu cuenta
Calibración de termómetros de resistencia.
La empresa Klasmeier ofrece calibraciones acreditadas según DIN EN ISO/IEC 17025 (DAkkS) para termorresistencias (p. ej. Pt100, Pt25). La calibración se realiza en puntos de temperatura fijos o mediante el método de comparación basado en la directiva DKD-R 5-1. El rango de calibración se extiende desde -196 °C hasta 962 °C y se alcanzan incertidumbres de medición de hasta el rango de mikelvin.
Ecuación de Callendar-Van Dusen
La ecuación de Callendar-Van Dusen es una fórmula utilizada para describir esta relación entre la temperatura y la resistencia eléctrica de un sensor de temperatura de resistencia de platino.
La ecuación de Callendar-Van Dusen también se conoce como “CVD” para abreviar y se utiliza desde la década de 1920. La curva característica está estandarizada en DIN EN 60751, que describe las termorresistencias industriales de platino y los sensores de temperatura de platino. Se publicó por primera vez en la década de 1990 y todavía es válida en su última revisión como DIN EN 60751:2009-05.
La propia ecuación de Callendar-Van Dusen se puede formular en dos partes, para temperaturas superiores e inferiores a 0 °C:
Para temperaturas T > 0 °C:

Para temperaturas T < 0 °C:
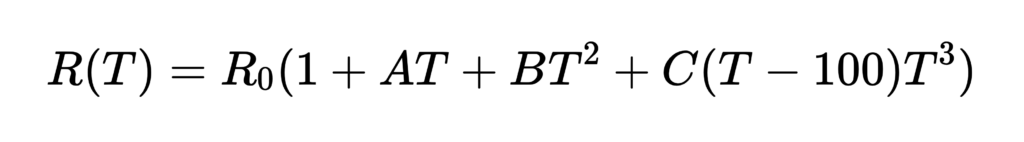
Aquí está:
- R(T) es la resistencia a la temperatura (T)
- R0 es la resistencia a 0 °C
- A, B y C son coeficientes que dependen de la termorresistencia de platino.
Los coeficientes de la ecuación de Callendar-Van Dusen están normalizados en DIN EN 60751:2009-05:
A=3.9083×10 −3°C-1
B=−5,775×10 −7 °C-2
C=−4.183×10 −12°C-4
Pero también es posible calibrar termómetros individuales y calcular coeficientes individuales. Esto tiene la ventaja de que ya no es necesario evaluar el termómetro en función de las desviaciones límite de la norma, sino que se puede adaptar individualmente a su propia curva característica.
La ecuación de Callendar-Van Dusen permite realizar mediciones de temperatura muy precisas sustituyendo la resistencia medida del termómetro en la ecuación de Callendar-Van Dusen y calculando la temperatura.
El siguiente gráfico muestra los dos rangos de temperatura de la ecuación de Callendar-Van Dusen. El rango de temperatura de -200 °C a 0 °C se muestra en azul y el rango de temperatura de 0 °C a 850 °C se muestra en rojo.
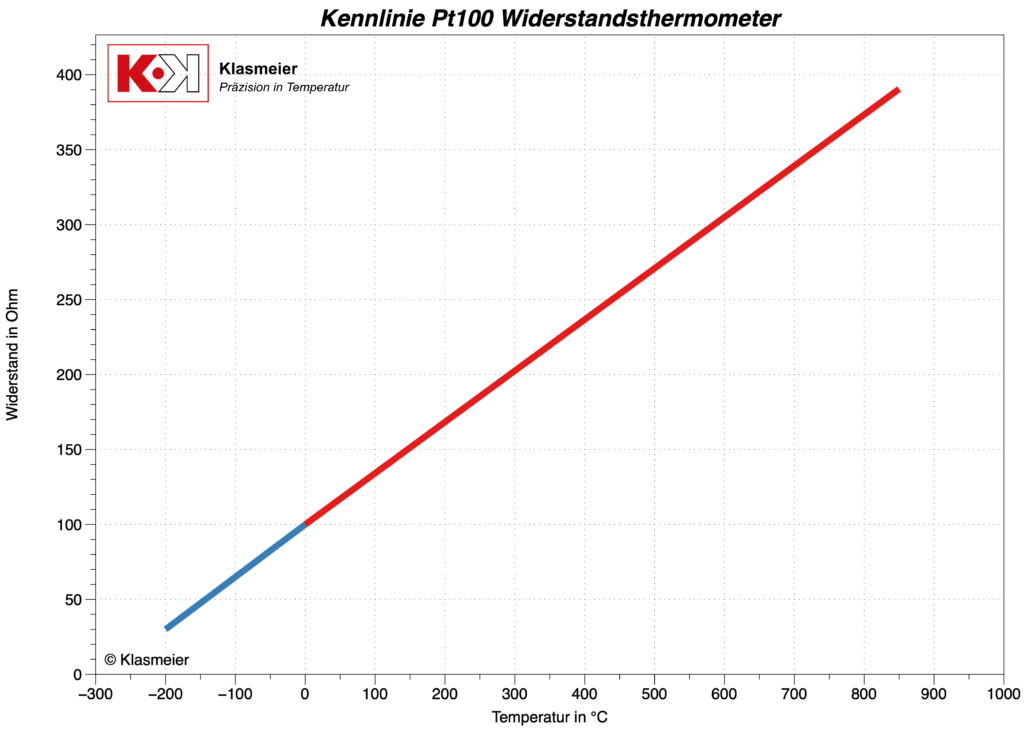
La resistencia nominal R0 de los termómetros de resistencia.
Para clasificar mejor las resistencias de medición, en la norma DIN EN 60751 se introdujo la denominada resistencia nominal R0 . Describe la resistencia eléctrica del sensor de temperatura a 0 °C. Por ejemplo, un sensor de temperatura Pt100 tiene una resistencia de 100 ohmios a 0°C. En la norma se enumeran las siguientes resistencias nominales:
- Pt 10 = 10 ohmios a 0 °C
- Pt 100 = 100 ohmios a 0 °C
- Pt 500 = 500 ohmios a 0 °C
- Pt 1.000 = 1.000 ohmios a 0 °C
En los termómetros de precisión se utilizan diferentes resistencias nominales, como Pt 25, Pt 2,5 o Pt 0,25, que a menudo cumplen los requisitos de ITS-90 . Estos se denominan entonces SPRT o termómetros estándar . Para aplicaciones de laboratorio, suelen preferirse los termómetros Pt 25 porque ofrecen un buen equilibrio entre estabilidad, sensibilidad y autocalentamiento.
Coeficiente de temperatura para termómetros de resistencia.
La diferencia entre los termómetros estandarizados y los termómetros normales según la ITS-90 se puede ver en el llamado coeficiente de temperatura, que se define en la norma mediante una medición de resistencia a 0 °C y 100 °C:
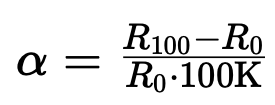
Esto significa:
alfa = aumento del termómetro en 1/K
R100 = resistencia a 100 °C en ohmios
R0 = resistencia a 0 °C en ohmios
El valor alfa de los sensores de temperatura industriales estándar es 3,85 10^-3/K, mientras que el valor alfa de los termómetros estándar según ITS-90 es 3,92875 10^-3/K. Este valor corresponde a la sensibilidad del platino espectralmente puro en este rango de temperatura.
Sensibilidad de los termómetros de resistencia.
La sensibilidad de un termómetro de resistencia describe cuánto cambia la resistencia del sensor en relación con un cambio de temperatura. Es una medida de la precisión con la que reacciona el sensor a los cambios de temperatura. Con Pt100, la resistencia cambia aproximadamente 0,385 ohmios por cada grado Celsius de cambio de temperatura. Esta tasa de cambio, conocida como coeficiente de temperatura, es una medida directa de la sensibilidad del sensor. La sensibilidad es crucial para la precisión y resolución del sensor. Un sensor con mayor sensibilidad puede detectar cambios de temperatura más pequeños y permite mediciones de temperatura más precisas. Esto es particularmente importante en aplicaciones donde se requiere un control preciso de la temperatura, como en laboratorios o control de procesos industriales.
Sin embargo, también hay que tener en cuenta que los sensores de temperatura con alta sensibilidad suelen tener un alto nivel de autocalentamiento y son menos estables a largo plazo. Por lo tanto, la relación entre el valor nominal y la sensibilidad de un sensor de temperatura debe elegirse con mucho cuidado.
Para conseguir una resistencia nominal definida se ajusta la longitud o el diámetro del hilo de platino en la resistencia de medición. Esto no sólo cambia la resistencia, sino también la sensibilidad de los sensores a aprox.
- Punto 10 = 0,04 ohmios/K
- Punto 100 = 0,4 ohmios/K
- Pt 500 = 2 ohmios/K
- Pt 1.000 = 4 ohmios/K

Por tu cuenta
Termómetro de precisión eXacal
Los termómetros de precisión eXacal de Klasmeier están diseñados para mediciones y calibraciones de temperatura precisas en un amplio rango de temperatura de -200 °C a 1200 °C. Disponibles como termómetros de resistencia y termopares de metales preciosos, ofrecen alternativas sólidas a los termómetros estándar ITS-90. Son adecuados tanto para aplicaciones industriales como para calibraciones de laboratorio y están hechos a mano en nuestra fábrica.
Tecnologías de conexión para termómetros de resistencia.
Las termorresistencias se pueden conectar a aparatos de medición, registradores de datos o puentes de medición, y existen diferentes métodos para ello.
- Tecnología de dos hilos
- Tecnología de tres hilos
- Tecnología de cuatro hilos
Tecnología de dos hilos
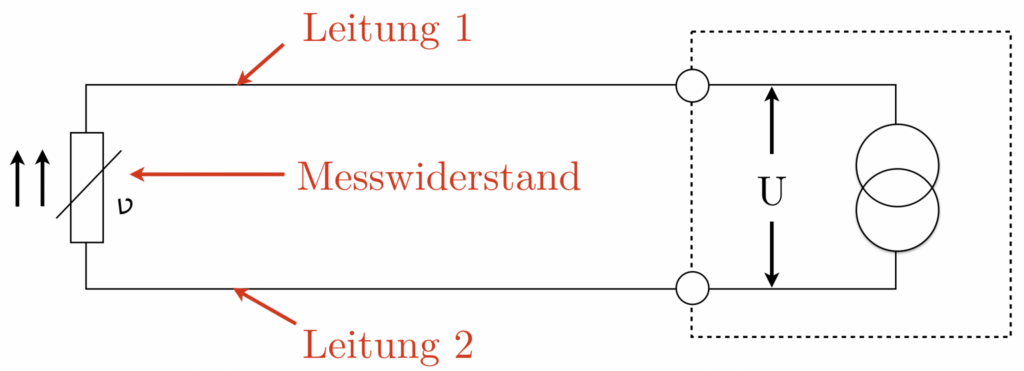
La técnica de dos hilos muestra cómo conectar un sensor de temperatura a un dispositivo de medición, como se muestra en la imagen. Es importante tener en cuenta la resistencia de los cables de conexión porque están conectados en serie con la resistencia de medición.
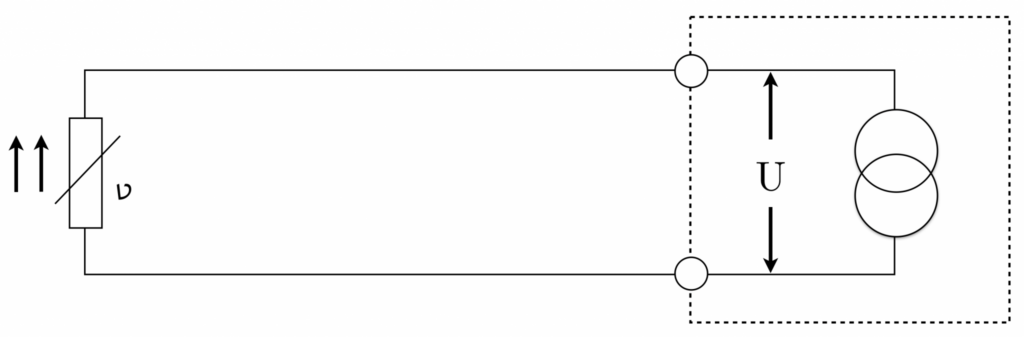
La medición resultante proviene de la suma de la resistencia de la línea 1, la resistencia de medición (el sensor de temperatura real) y la línea 2, lo que resulta en una medición aumentada. Por tanto, es esencial corregir el resultado de la medición para eliminar errores de medición.
Un ejemplo de cálculo ejemplar demuestra el alcance de la desviación de medición en determinadas condiciones de aplicación. Suponga que un sensor de temperatura está conectado mediante un cable de cobre en las siguientes condiciones especificadas:
- Resistencia específica de la línea de cobre a temperatura ambiente: 0,017
- Sección transversal del cable: 0,5 mm^2
- Longitud del cable: aprox. 50 m
La desviación de medición debida al cable de conexión se puede determinar mediante la ecuación
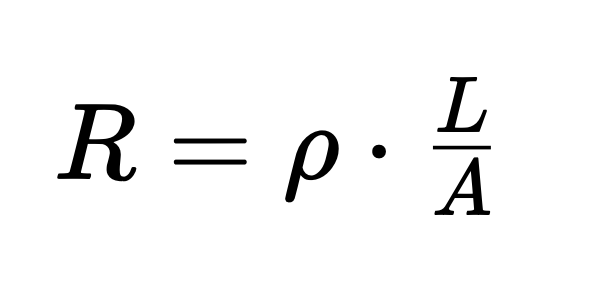
determinarse, mediante la cual:
- R es la resistencia del conductor,
- \rho la resistencia específica,
- L es la longitud del conductor y
- A representa el área de la sección transversal.
En este contexto se obtiene una resistencia del conductor de 3,4 ohmios:
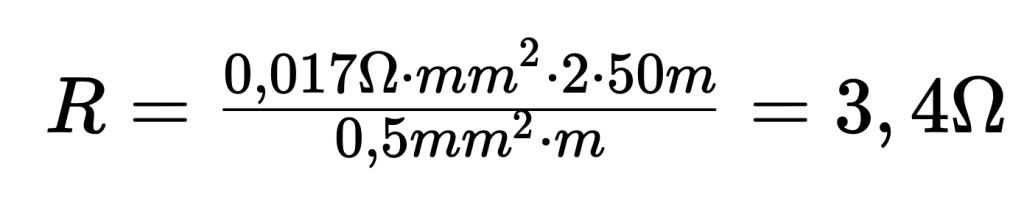
Teniendo en cuenta una sensibilidad (E) de un sensor de temperatura PT 100 de aprox. 0,385 ohmios/K, se obtiene una desviación de medición de 8,8 K.
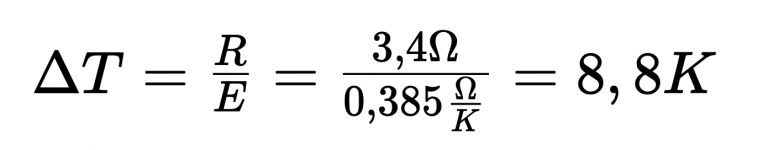
La longitud de la línea de aproximadamente 50 m debe tenerse en cuenta dos veces para el “camino de ida” (línea 1) y para el “camino de regreso” (línea 2).
Históricamente, era bastante convencional conectar termómetros en las plantas de producción mediante tecnología de dos hilos. Antes de la era de la tecnología digital que facilitaba la corrección de errores sistemáticos, se utilizaban tablas de corrección para lograr mediciones precisas.
Un ejemplo ilustra los valores de corrección para un cable de conexión de 10 m de longitud en función de la sección del cable.
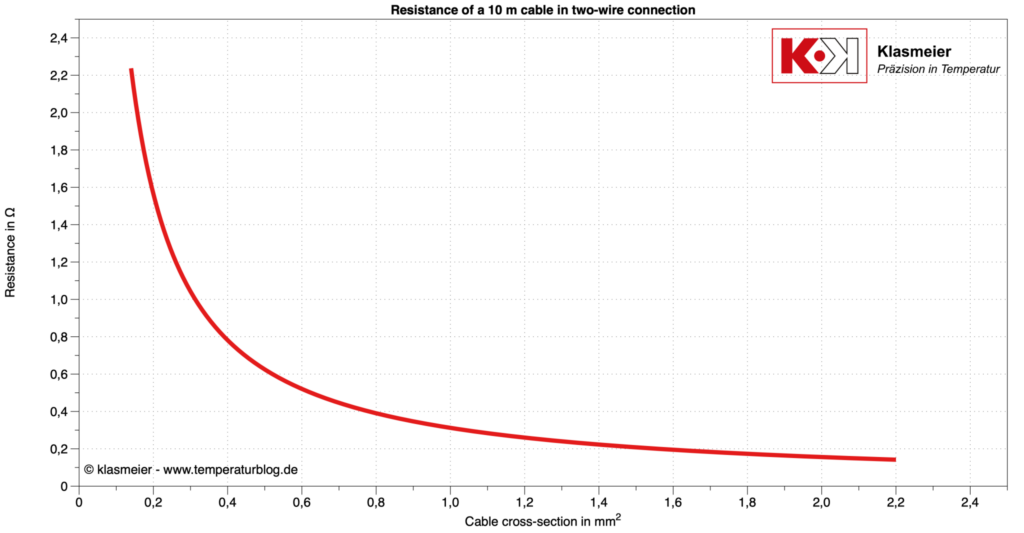
Con un cable de conexión con una sección de 0,5 mm^2, la resistencia en un circuito de dos hilos de 10 m de longitud es de 0,6 ohmios. Esto implica que los valores medidos deben corregirse por este factor. Para un Pt100 esto corresponde a unos 1,6 °C.
El siguiente gráfico muestra los valores de corrección para un Pt100 en relación con la sección transversal de un cable de cobre de 10 m de longitud utilizando tecnología de dos hilos.
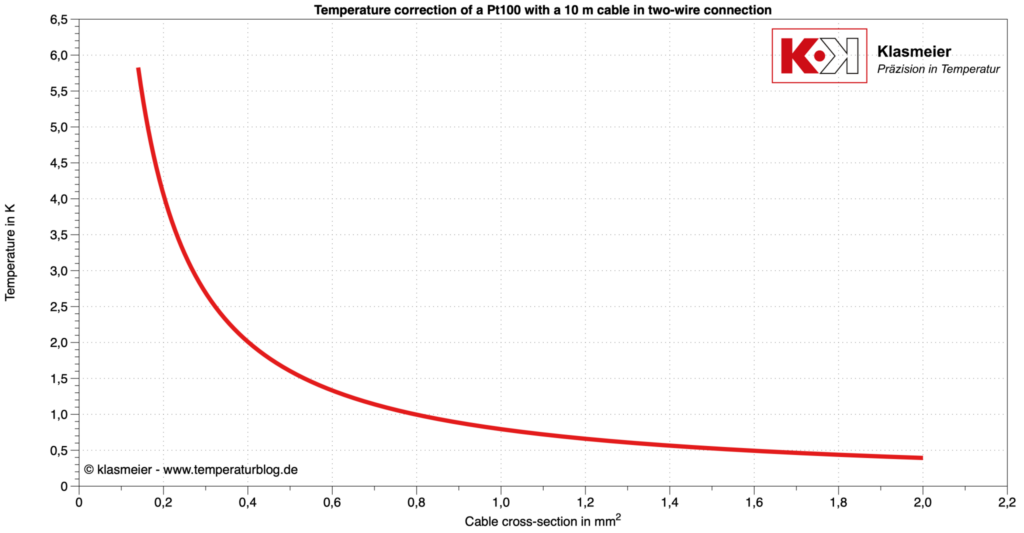
Tecnología de tres hilos
La tecnología de tres hilos representa una optimización en comparación con la tecnología de dos hilos, especialmente en lo que respecta a minimizar los errores de medición debidos a la resistencia de la línea. En esta configuración se utilizan tres líneas, dos líneas conectadas en paralelo a la resistencia de medición y una tercera línea para compensar la resistencia de la línea.
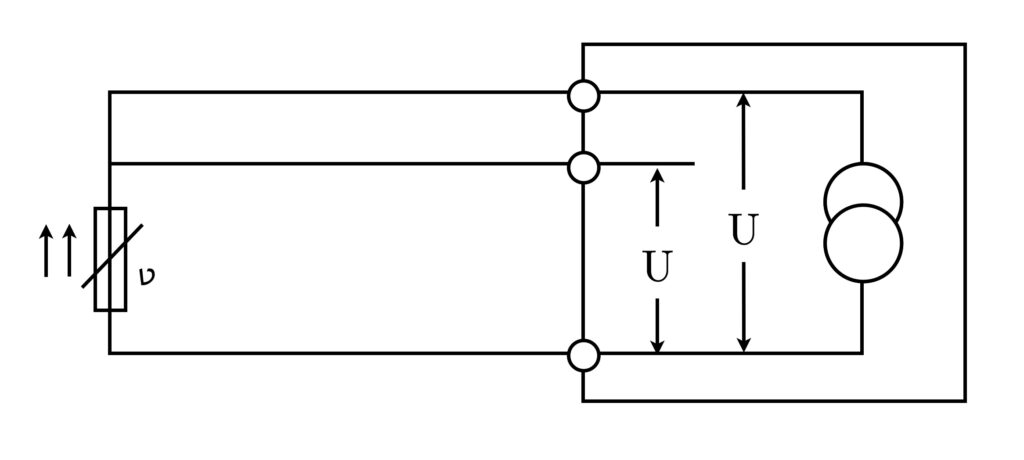
La resistencia del cable se compensa mediante el puente de medición, que tiene en cuenta la resistencia del tercer cable y resta así la resistencia total de los cables de conexión. Esto da como resultado una medición más precisa de la resistencia de medición real, ya que se minimizan las influencias de los cables de conexión.
Aunque la tecnología de tres hilos representa una mejora significativa con respecto a la tecnología de dos hilos, todavía es susceptible a errores debido a cambios de temperatura y diferentes longitudes de línea, lo que puede afectar la compensación de la resistencia de la línea.
Tecnología de cuatro hilos
La técnica de cuatro hilos, también conocida como medición de cuatro hilos Kelvin, representa una optimización adicional en la precisión de la medición de resistencia, especialmente para aplicaciones donde se requiere la mayor precisión. Esta técnica utiliza dos líneas adicionales para entregar la corriente de medición y medir la caída de voltaje a través del sensor, eliminando la influencia de la resistencia de la línea.
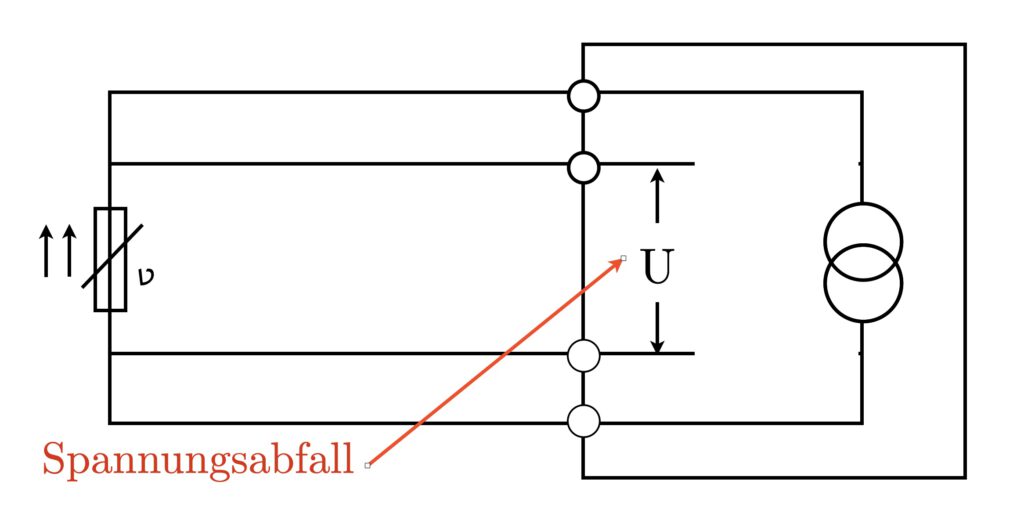
En esta configuración, la corriente de medición fluye a través de dos de las líneas (líneas de alimentación), mientras que las otras dos líneas (líneas de voltaje) se usan para medir la caída de voltaje directamente a través del sensor. Dado que la corriente de medición no fluye a través de las líneas de tensión, la resistencia de estas líneas no se incluye en la medición, lo que conduce a una mayor precisión de la medición.
La tecnología de cuatro hilos es especialmente ventajosa para aplicaciones con valores de resistencia bajos y longitudes de cable largas, ya que permite mediciones precisas sin la influencia de la resistencia del cable.
En resumen, las técnicas de tres y cuatro cables proporcionan mayor precisión y confiabilidad en comparación con la técnica de dos cables al minimizar o eliminar la influencia de la resistencia de la línea. La elección de la tecnología adecuada depende de los requisitos específicos de la aplicación, como la precisión de la medición, las condiciones ambientales y las consideraciones económicas.

Por tu cuenta
Termómetro de precisión de alta temperatura modelo Pt100 HS (0 °C a 850 °C)
El termómetro de precisión para altas temperaturas Pt100 de Klasmeier es adecuado para mediciones precisas de hasta 850 °C. Equipado con una protección cerámica hermética a los gases y una resistencia de medición Pt100 hecha a mano, ofrece incertidumbres de medición bajas. Ideal para usar como estándar de calibración. Disponible opcionalmente con calibración acreditada según DIN EN ISO/IEC 17025 (DAkkS).
Fuentes
- Frank Bernhard: Manual de medición técnica de temperatura, segunda edición
- Thomas Klasmeier: Libro de mesa “Temperatura”, edición 3
- Termómetros de resistencia industriales de platino y sensores de temperatura de platino (IEC 60751:2022)
- Termómetro de punta de cobre ISOTECH nº 108462 hasta casi 1100°C.
- Resistencia específica
- DIN 43760
- ley de ohm


