Motståndstermometer: Funktionssätt och användning

Pt100-motståndstermometrar är precisa temperaturgivare som används flitigt i en mängd industriella och vetenskapliga tillämpningar. Deras princip bygger på variationen i elektriskt motstånd hos en platina-tråd beroende på temperaturen. ”Pt” i Pt100 står för platina, materialet som tråden består av, och ”100” anger att motståndet vid 0 °C är exakt 100 ohm.

Pt100-motståndstermometrar erbjuder ett brett temperaturområde, från -200 °C till +850 °C, och kännetecknas av sin höga noggrannhet. Deras motstånd-temperatur-kurva är nästan linjär, vilket underlättar kalibrering och tolkning av de uppmätta värdena.

Dessa givare ändrar sitt elektriska motstånd proportionellt mot temperaturförändringen. Temperaturkoefficienten är cirka 0,385 ohm/°C vid 0 °C. Pt100-givare har vanligtvis två, tre eller fyra anslutningar. Följaktligen kan de användas i olika kopplingskonfigurationer, inklusive 2-ledar-, 3-ledar- och 4-ledar-koppling.

För att säkerställa noggranna mätningar måste Pt100-motståndstermometrar skyddas mot yttre påverkan som fukt och mekanisk belastning. Detta görs ofta genom användning av skyddsrör. Dessutom bör de kalibreras regelbundet, antingen i specialiserade laboratorier eller med hjälp av referenstermometrar.

Pt100-givare används i många tillämpningar, inklusive livsmedelsindustrin, laboratorier, klimatteknik, bilindustrin och kemisk processteknik.

Hur fungerar motståndstermometrar?

Motståndstermometrar används ofta för precisa temperaturmätningar. Det vanliga temperaturområdet ligger mellan cirka -50 °C och 600 °C, även om det finns specialtillämpningar där motståndstermometrar används från -200 °C till över 1000 °C. Den avbildade Pt100-motståndstermometern kommer från Klasmeiers kalibreringslaboratorium.

Mätprincipen för dessa termometrar baseras på mätning av det elektriska motståndet hos mätmotstånd, för vilket Ohms lag är grundläggande:

U = R ⋅ I = konstant

där:
U = spänning,
R = motstånd,
I = ström

I skolundervisningen framställs Ohms lag ofta som en triangel som tydliggör sambandet mellan ström, spänning och motstånd.

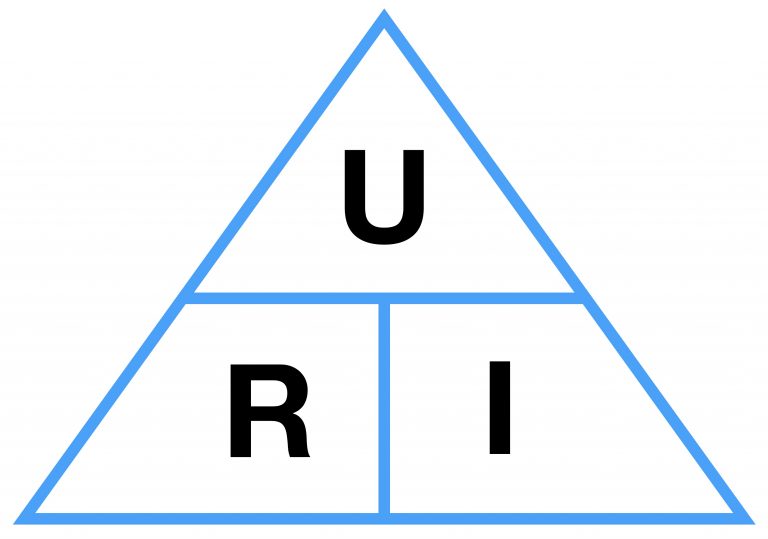
Om två av dessa storheter är kända kan den tredje beräknas. I kopplingsschemat visas Ohms lag som i följande grafik.

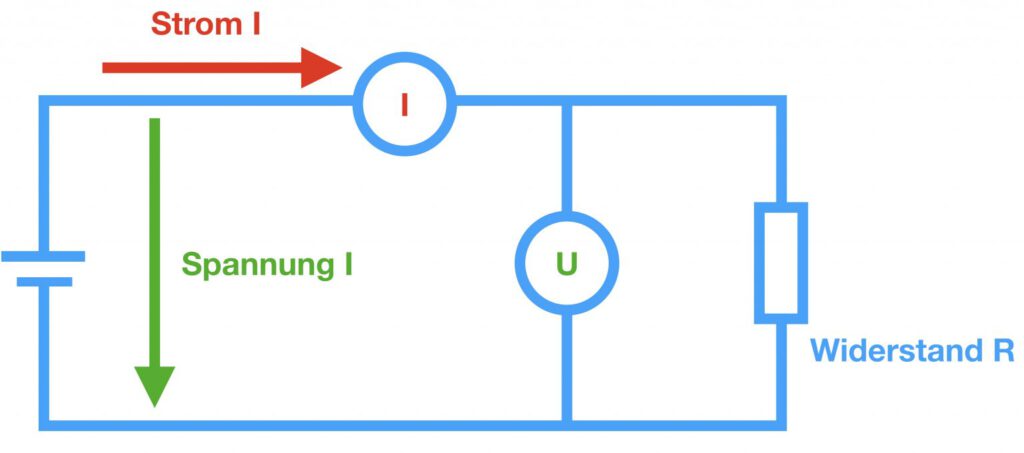
Sambanden för motståndsmätning och därmed för motståndstermometrar kan också visas grafiskt i en bild.

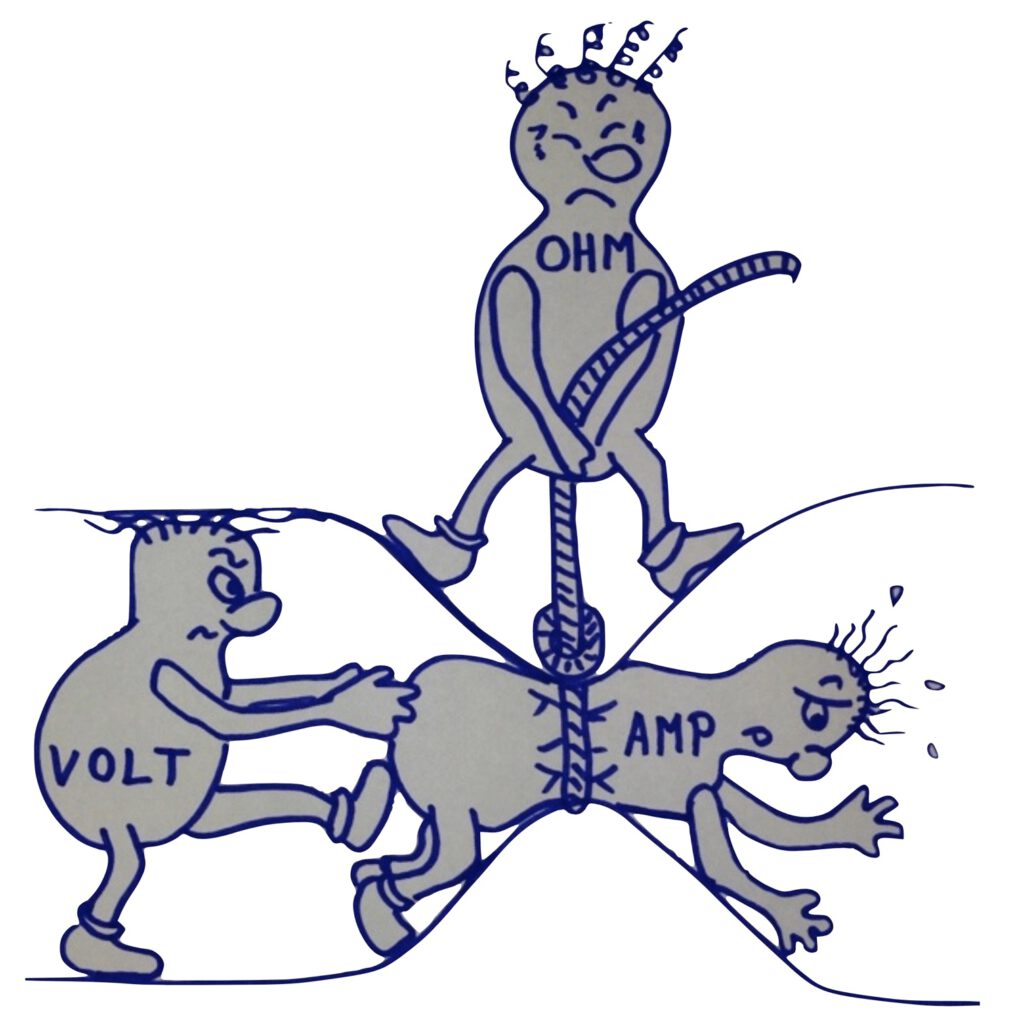
Här trycks ”VOLT-gubben” (U – spänning) av ”AMP-gubben” (I – ström) genom ett rör, medan ”OHM-gubben” (R – motstånd) försöker förhindra detta genom att minska rörets diameter. ”OHM-gubbens” framgång är temperaturberoende: Ju varmare det är, desto svårare blir det för ”VOLT-gubben” att flytta ”AMP-gubben”. Eftersom denna temperaturberoende effekt är reproducerbar kan principen för elektrisk motståndsmätning användas för temperaturmätning. Ett uppmätt motstånd R i ohm omvandlas via ett känt samband till en temperatur T i °C eller K.

I princip kan varje elektrisk ledare för vilken Ohms lag gäller användas som termometer. Det specifika motståndet är den fysikaliska konstanten som beskriver denna egenskap. En översikt visar de olika specifika motstånden för material vid 20 °C.

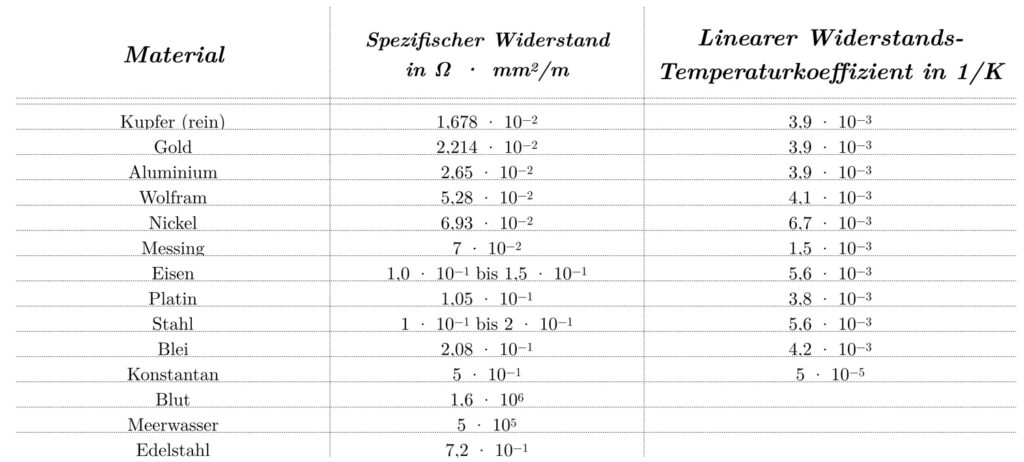
Även om alla nämnda material i grunden kan användas för temperaturmätning finns det vissa urvalskriterier för materialvalet av termometrar. Materialet bör ha ett högt specifikt motstånd och vara lämpligt i grunden. Till exempel har mänskligt blod med 1,6×106 Ω⋅mm2 /m ett utmärkt specifikt motstånd, men är inte lämpligt för industriell tillverkning av termometrar. Metaller är mer lämpliga för detta ändamål.

Förutom det specifika motståndet är även den linjära motstånd-temperaturkoefficienten viktig. Denna beskriver ändringen av ett materials motstånd per grad Celsius och anges i 1/K. Den kan också kallas känslighet. För att minimera kraven på mättekniken bör denna koefficient vara så stor som möjligt. Det gäller alltså att hitta den bästa kompromissen mellan kostnad, materialets grundläggande lämplighet, specifikt motstånd och motstånd-temperaturkoefficient.

Nickel och platina har visat sig vara lämpliga material. Inledningsvis ansågs nickel-mätmotstånd, som t.ex. Ni100, vara favoriter eftersom de hade en högre känslighet än platina-mätmotstånd. De visade dock högre gränsavvikelser och ett begränsat temperaturområde. Standarden för nickeltermometrar, DIN 43760, drogs tillbaka på 1990-talet. Sedan dess används nickel-mätmotstånd huvudsakligen i tekniska specialtillämpningar.

Med tiden har platina-mätmotstånd, som t.ex. Pt100, slagit igenom. De är vanliga inom industriell mätteknik och är idag standarden för elektrisk temperaturmätning med motståndstermometrar.

Pt100-karakteristiken för motståndstermometrar förklarad på ett enkelt sätt

Platinagivare har etablerat sig som motståndstermometrar. Sambandet mellan temperaturen och motståndet hos platinatermometrar beskrivs inte proportionellt, utan med ett polynom av högre ordning:

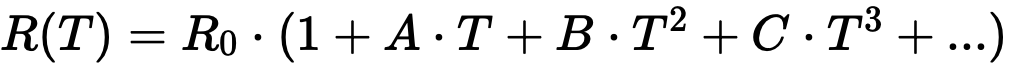
Här betyder:

R(T) = Termometerns motstånd
R0 = Termometerns motstånd vid 0 °C
A, B, C, … = Individuella parametrar för termometern eller norm
T = Temperatur

Callendar-Van Dusen-ekvationen

Callendar-Van Dusen-ekvationen är en formel som används för att beskriva detta samband mellan temperaturen och det elektriska motståndet hos en platina-motståndstemperaturgivare.

Callendar-Van-Dusen-ekvationen förkortas även som ”CVD” och har använts sedan 1920-talet. Karakteristiken är standardiserad i DIN EN 60751, som beskriver industriella platina-motståndstermometrar och platina-temperaturgivare. Den publicerades första gången på 1990-talet och är i sin senaste revidering som DIN EN 60751:2009-05 fortfarande giltig.

Callendar-Van-Dusen-ekvationen själv kan formuleras i två delar, för temperaturer över och under 0 °C:

För temperaturer T > 0 °C:

För temperaturer T 0 °C:

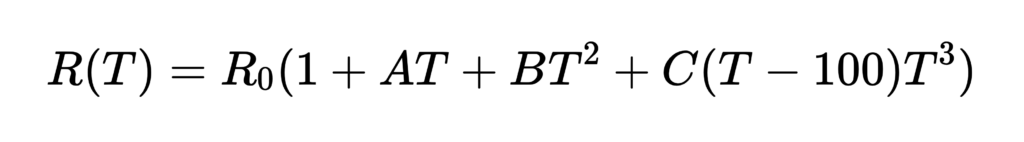
Här är:

• R(T) motståndet vid temperaturen ( T )
• R0 motståndet vid 0 °C
• A, B och C är koefficienter som beror på platina-motståndstermometern

I DIN EN 60751:2009-05 är koefficienterna för Callendar-Van-Dusen-ekvationen standardiserade:

A=3,9083×10 −3 °C-1
B=−5,775×10 −7 °C-2
C=−4,183×10 −12 °C-4

Det är dock också möjligt att kalibrera enskilda termometrar och beräkna individuella koefficienter. Detta har fördelen att termometern inte längre behöver bedömas utifrån standardens gränsavvikelser, utan kan anpassas individuellt till sin egen karakteristik.

Callendar-Van-Dusen-ekvationen gör det möjligt att utföra mycket precisa temperaturmätningar genom att sätta in termometerns uppmätta motstånd i Callendar-Van-Dusen-ekvationen och beräkna temperaturen.

Följande grafik visar de två temperaturområdena för Callendar-Van-Dusen-ekvationen. Blått visar temperaturområdet från -200 °C till 0 °C och temperaturområdet från 0 °C till 850 °C visas i rött.

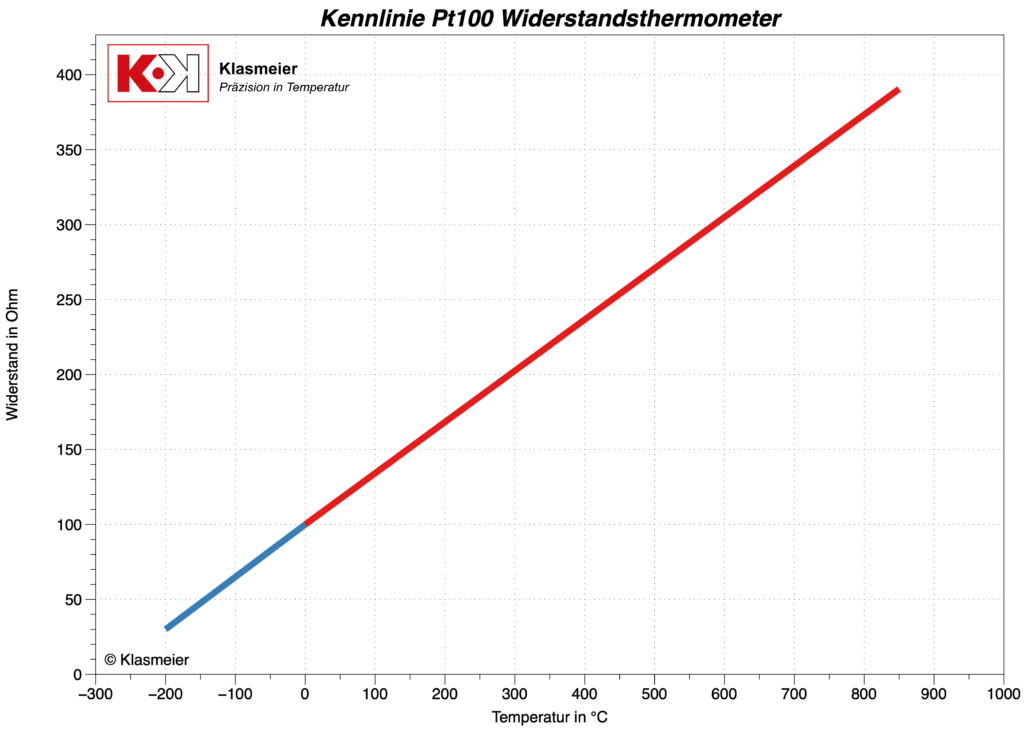
Nollmotståndet R0 för motståndstermometrar

För att bättre klassificera mätmotstånden infördes det så kallade nollmotståndet R0 i standarden DIN EN 60751. Detta beskriver det elektriska motståndet hos temperaturgivaren vid 0 °C. Till exempel har en Pt100-temperaturgivare ett motstånd på 100 ohm vid 0 °C. I standarden anges följande nollmotstånd:

• Pt 10 = 10 ohm vid 0 °C
• Pt 100 = 100 ohm vid 0 °C
• Pt 500 = 500 ohm vid 0 °C
• Pt 1 000 = 1 000 ohm vid 0 °C

Avvikande nollmotstånd som Pt 25, Pt 2,5 eller Pt 0,25 används vid precisions-termometrar och uppfyller ofta kraven i ITS-90. Dessa betecknas då som SPRT eller normal-termometer. Vid laboratorietillämpningar föredras ofta Pt 25-termometrar, eftersom de erbjuder en bra kompromiss mellan stabilitet, känslighet och egenuppvärmning.

Temperaturkoefficient vid motståndstermometrar

Skillnaden mellan standardiserade termometrar och normal-termometrar enligt ITS-90 visar sig i den så kallade temperaturkoefficienten, som i standarden definieras genom en motståndsmätning vid 0 °C och 100 °C:

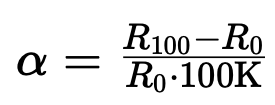
Här betyder:

alpha = Termometerns ökning i 1/K
R100 = Motstånd vid 100 °C i ohm
R0 = Motstånd vid 0 °C i ohm

Alfa-värdet för industriella temperaturgivare enligt standard är 3,85 10^-3/K, medan alfa-värdet för normal-termometrar enligt ITS-90 är 3,92875 10^-3/K. Detta värde motsvarar känsligheten hos spektralren platina i detta temperaturområde.

Känslighet vid motståndstermometrar

Känsligheten hos en motståndstermometer beskriver hur mycket givarens motstånd ändras i förhållande till en temperaturförändring. Det är ett mått på hur exakt givaren reagerar på temperaturförändringar. För Pt100 ändras motståndet med cirka 0,385 ohm för varje grad Celsius temperaturförändring. Denna ändringshastighet, känd som temperaturkoefficienten, är ett direkt mått på givarens känslighet. Känsligheten är avgörande för givarens noggrannhet och upplösning. En givare med högre känslighet kan detektera mindre temperaturförändringar och möjliggör mer exakta temperaturmätningar. Detta är särskilt viktigt i tillämpningar där exakt temperaturkontroll krävs, som i laboratorier eller i processstyrning inom industrin.

Det är dock också viktigt att notera att temperaturgivare med stor känslighet ofta har en hög egenuppvärmning och uppvisar mindre långtidsstabilitet. Därför måste förhållandet mellan nominellt värde och känslighet hos en temperaturgivare väljas mycket noggrant.

För att uppnå ett definierat nollmotstånd anpassas längden eller diametern på platina-tråden i mätmotståndet. Detta ändrar inte bara motståndet, utan också givarnas känslighet till ca:

• Pt 10 = 0,04 ohm / K
• Pt 100 = 0,4 ohm / K
• Pt 500 = 2 ohm / K
• Pt 1 000 = 4 ohm / K

Anslutningstekniker för motståndstermometrar

Motståndstermometrar kan anslutas till mätinstrument, dataloggrar eller mätbryggor, och det finns olika tekniker för detta.

• Tvåledarteknik
• Treledarteknik
• Fyrledarteknik

Tvåledarteknik

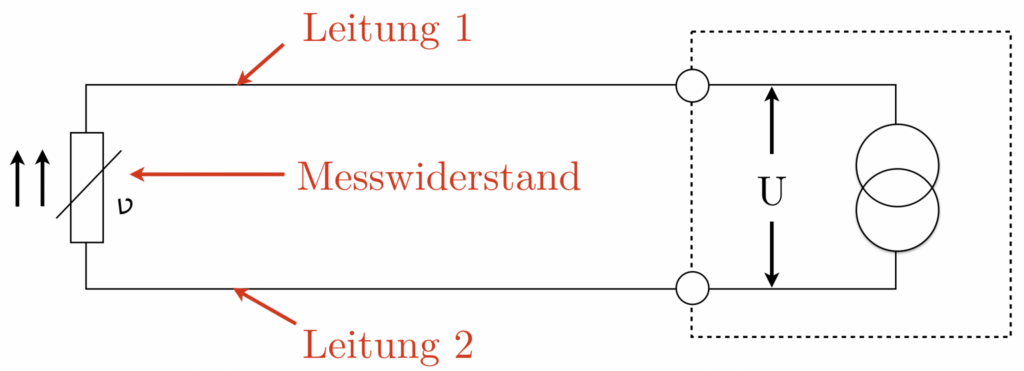
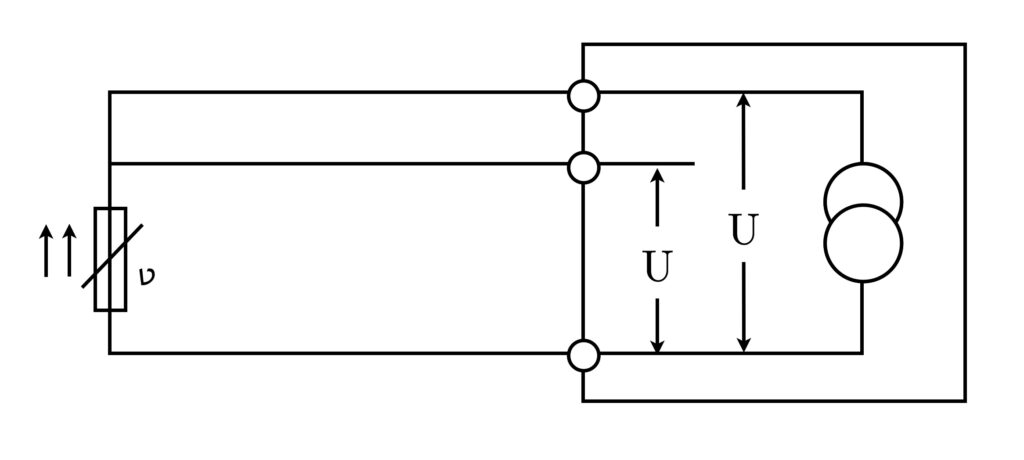
Tvåledartekniken visar hur man ansluter en temperaturgivare till ett mätinstrument, som det kan ses på bilden. Det är viktigt att motståndet i anslutningskablarna beaktas, eftersom det är seriekopplat med mätmotståndet.

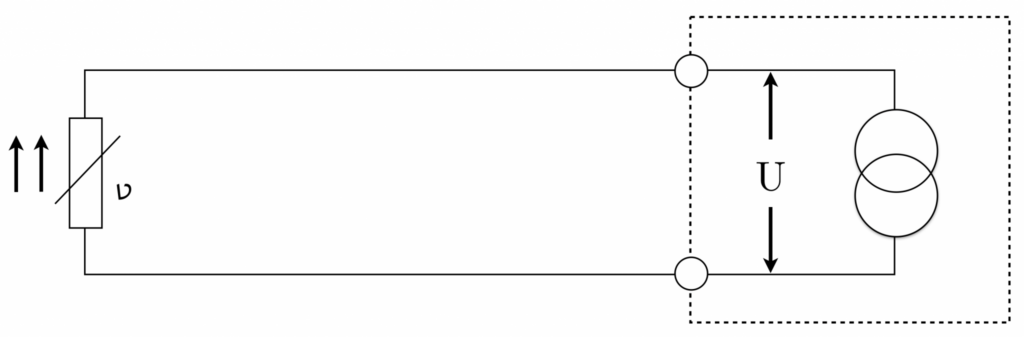
Den resulterande mätningen erhålls från summeringen av motståndet från ledning 1, mätmotståndet (den faktiska temperaturgivaren) och ledning 2, vilket leder till en ökad mätning. Därför är en korrigering av mätresultatet absolut nödvändig för att eliminera mätfel.

Ett exemplariskt beräkningsexempel visar omfattningen av mätavvikelsen under vissa tillämpningsförhållanden. Antag att en temperaturgivare är ansluten med hjälp av en kopparledning, under följande specificerade förhållanden:

• Specifikt motstånd för kopparledningen vid rumstemperatur: 0,017
• Ledningens tvärsnitt: 0,5 mm^2
• Ledningens längd: ca 50 m

Mätavvikelsen på grund av anslutningsledningen kan beräknas med hjälp av ekvationen

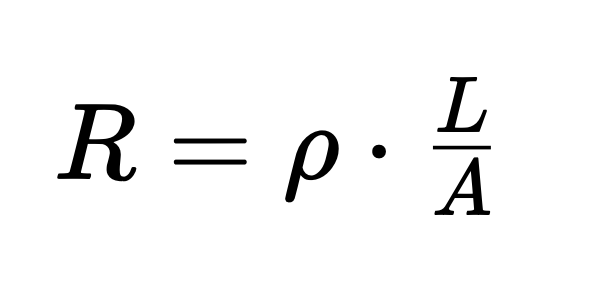
där:

• R representerar ledningsmotståndet,
• ho representerar det specifika motståndet,
• L representerar ledningslängden och
• A representerar tvärsnittsytan.

I detta sammanhang resulterar ett ledningsmotstånd på 3,4 ohm:

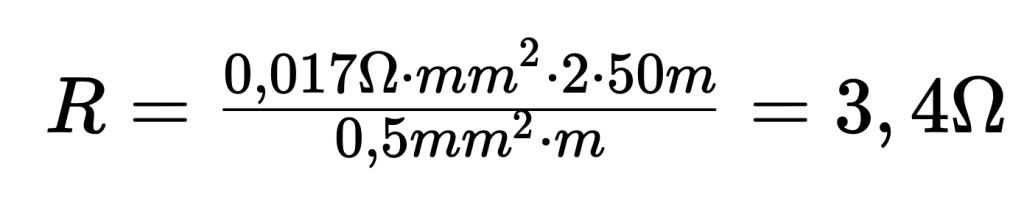
Med beaktande av en känslighet ( E ) hos en PT 100 temperaturgivare på ca 0,385 ohm / K, erhålls en mätavvikelse på 8,8 K.

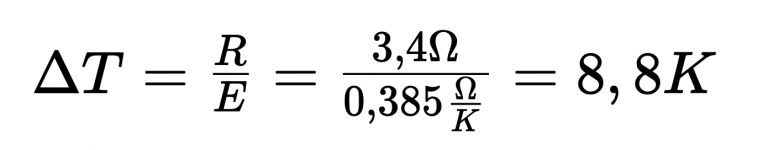
Ledningslängden på ca 50 m måste beaktas två gånger för både ”framvägen” (ledning 1) och för ”återvägen” (ledning 2).

Historiskt sett var det ganska konventionellt att ansluta termometrar i produktionsanläggningar med hjälp av tvåledartekniken. Före den digitala teknologins era, som förenklar korrigeringen av systematiska fel, användes korrigeringstabeller för att uppnå noggranna mätvärden.

Ett exempel illustrerar korrigeringsvärden för en 10 m lång anslutningsledning beroende på ledningens tvärsnitt.

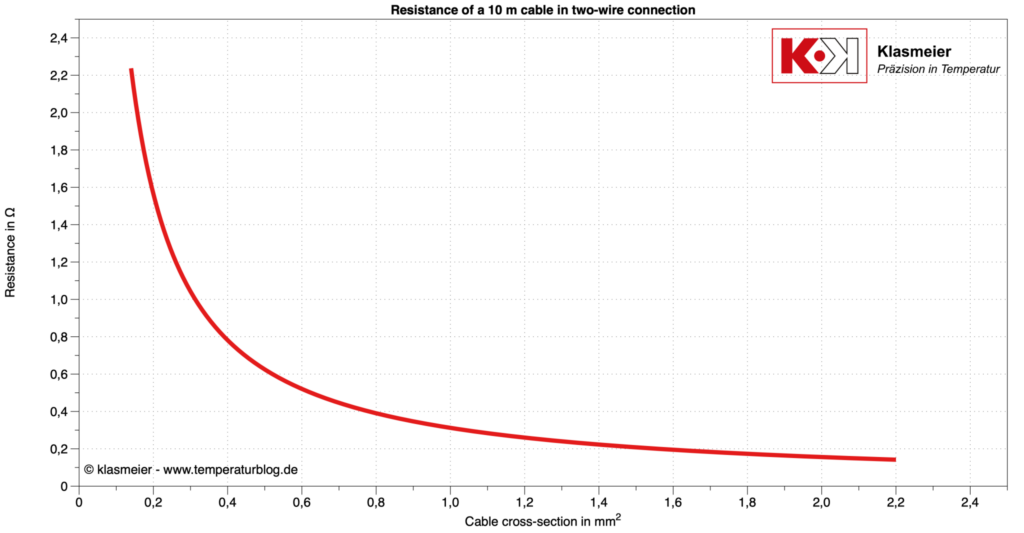
För en anslutningsledning med en ledningstvärsnitt på 0,5 mm^2 är motståndet i en 10 m lång tvåledarkoppling 0,6 ohm. Detta innebär att mätvärdena måste korrigeras med denna faktor. För en Pt100 motsvarar detta cirka 1,6 °C.

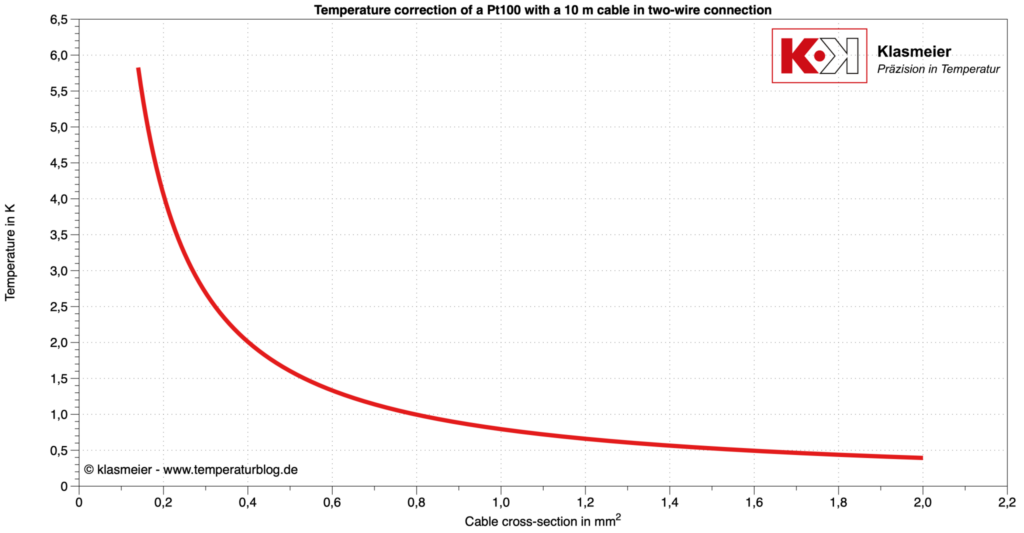
I följande grafik visas korrigeringsvärdena för en Pt100 i förhållande till tvärsnittet av en 10 m lång kopparledning i tvåledartekniken.

Treledarteknik

Treledartekniken är en optimering jämfört med tvåledartekniken, särskilt med avseende på minimering av mätfel på grund av ledningsmotstånd. I denna konfiguration används tre ledningar, varvid två ledningar är kopplade parallellt med mätmotståndet och en tredje ledning används för att kompensera för ledningsmotståndet.

Kompensationen av ledningsmotståndet sker genom mätbryggan, som beaktar motståndet i den tredje ledningen och därmed subtraherar det totala motståndet i anslutningsledningarna. Detta resulterar i en mer exakt mätning av det faktiska mätmotståndet, eftersom påverkan från anslutningsledningarna minimeras.

Även om treledartekniken är en betydande förbättring jämfört med tvåledartekniken är den fortfarande känslig för fel på grund av temperaturförändringar och olika ledningslängder, vilket kan påverka kompensationen av ledningsmotståndet.

Fyrledarteknik

Fyrledartekniken, även känd som Kelvin-fyrledarmätning, representerar en ytterligare optimering av precisionen i motståndsmätningen, särskilt för tillämpningar där högsta noggrannhet krävs. Denna teknik använder två extra ledningar för att leverera mätströmmen och mäta spänningsfallet över givaren, vilket eliminerar påverkan från ledningsmotståndet.

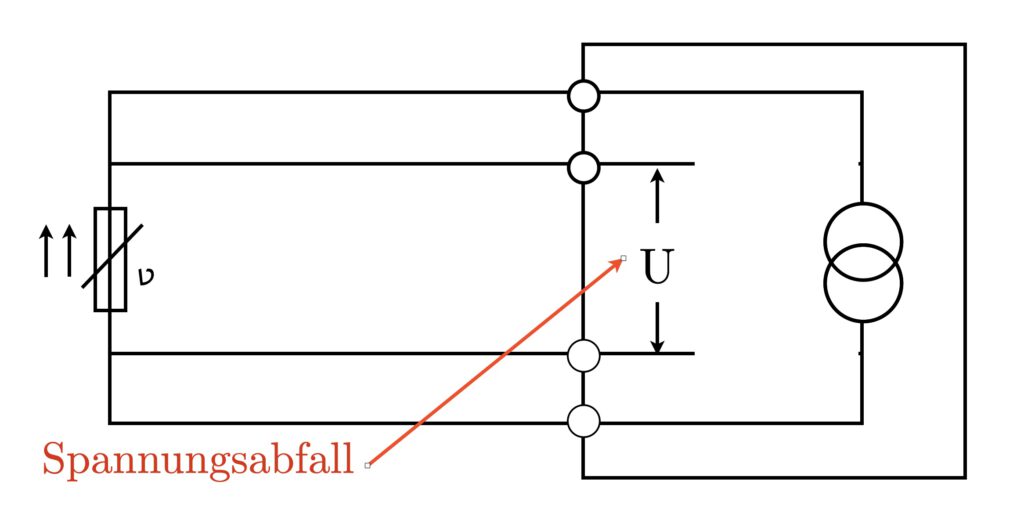
I den här konfigurationen flyter mätströmmen genom två av ledningarna (strömledningar), medan de andra två ledningarna (spänningsledningar) används för att mäta spänningsfallet direkt över sensorn. Eftersom mätströmmen inte flyter genom spänningsledningarna inkluderas inte ledningsresistansen i dessa ledningar i mätningen, vilket leder till högre mätnoggrannhet.

Fyrledartekniken är särskilt fördelaktig för applikationer med låga resistansvärden och långa ledningslängder, eftersom den möjliggör en exakt mätning som är fri från påverkan av ledningsresistanser.

Sammanfattningsvis erbjuder tre- och fyrledarteknikerna förbättrad noggrannhet och tillförlitlighet jämfört med tvåledartekniken genom att minimera eller eliminera påverkan av ledningsresistanser. Valet av lämplig teknik beror på de specifika kraven i applikationen, såsom mätnoggrannhet, omgivningsförhållanden och ekonomiska överväganden.

Källor

• Frank Bernhard: Handbuch der Technischen Temperaturmessung, 2. Auflage
• Thomas Klasmeier: Tabellenbuch „Temperatur“, Ausgabe 3
• Industriella platinamotståndstermometrar och platina temperaturgivare (IEC 60751:2022)
• ISOTECH Kopparpunkt-termometer Nr. 108462 till nästan 1100°C.
• Specifikt motstånd
• DIN 43760
• Ohms lag