The International Temperature Scale of 1990 (ITS-90)

The International Temperature Scale of 1990 (ITS-90) is a globally recognized temperature scale introduced by the International Committee for Weights and Measures (CIPM). It serves as a global standard for precise temperature measurements and is based on the concept of thermodynamic temperature. The ITS-90 is a revised version of the previous International Practical Temperature Scale of 1968 (IPTS-68).

The ITS-90 uses various precisely defined temperature fixed points and interpolation methods to determine temperatures. Temperature fixed points are the temperatures of phase transitions of certain substances, such as freezing points or triple points.

The ITS-90 uses the Kelvin scale (K) as its unit, replacing the Celsius scale used in IPTS-68. However, both units continue to be used, with 1 Kelvin degree and 1 Celsius degree having the same magnitude, and the Celsius zero point being at 273.15 K.

To convert from the Kelvin scale (K) to the Celsius scale (°C), simply subtract 273.15 from the temperature in Kelvin: T(°C) = T(K) – 273.15.

Temperature Fixed Points of ITS-90

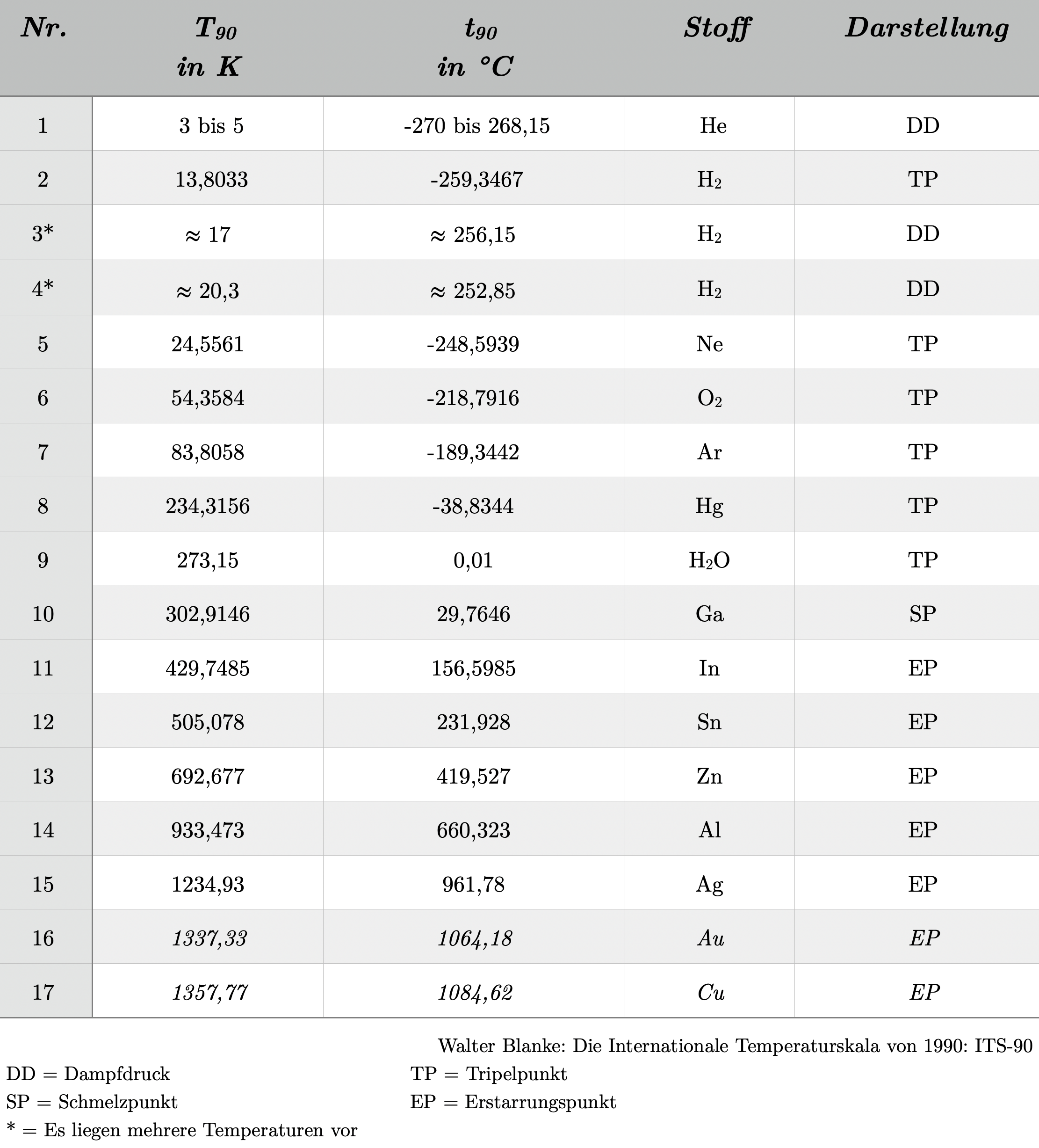
The International Temperature Scale of 1990 (ITS-90) uses various “temperature fixed points” as defined temperatures. A temperature fixed point is a temperature characterized by a specific, reproducible physical event, such as a phase change of a particular substance.

The International Temperature Scale of 1990 (ITS-90) uses triple points, melting points, and freezing points:

• Triple point: The triple point of a substance is the unique temperature and pressure at which the three phases of a substance – solid, liquid, and gaseous – can exist in equilibrium. At this specific temperature and pressure combination, a substance can exist simultaneously as a solid, liquid, and gas. A well-known example of a triple point is that of water, which occurs at a temperature of 0.01 °C (273.16 K) and a specific pressure of 611.657 Pascal.
• Melting point: The melting point is the temperature at which a solid substance begins to melt and transition into a liquid state. This temperature is specific to each substance and is measured under normal pressure. For example, the ITS-90 uses the melting point of gallium, which is at 29.7646 °C.
• Freezing point: The freezing point is the temperature at which a liquid begins to solidify and transition into a solid state. For example, the freezing point of aluminum is at 660.323 °C.

Here are the main temperature fixed points used by ITS-90:

The Calibration Ranges of ITS-90

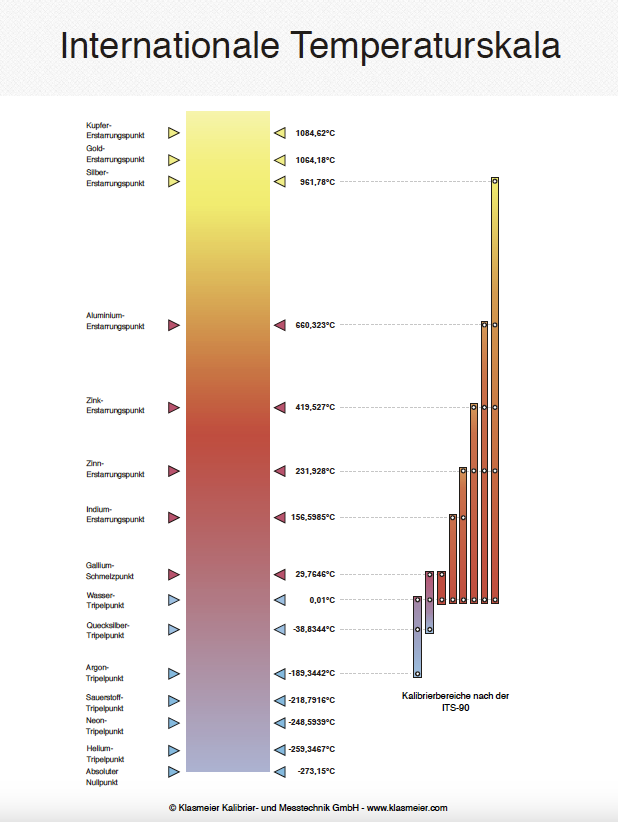
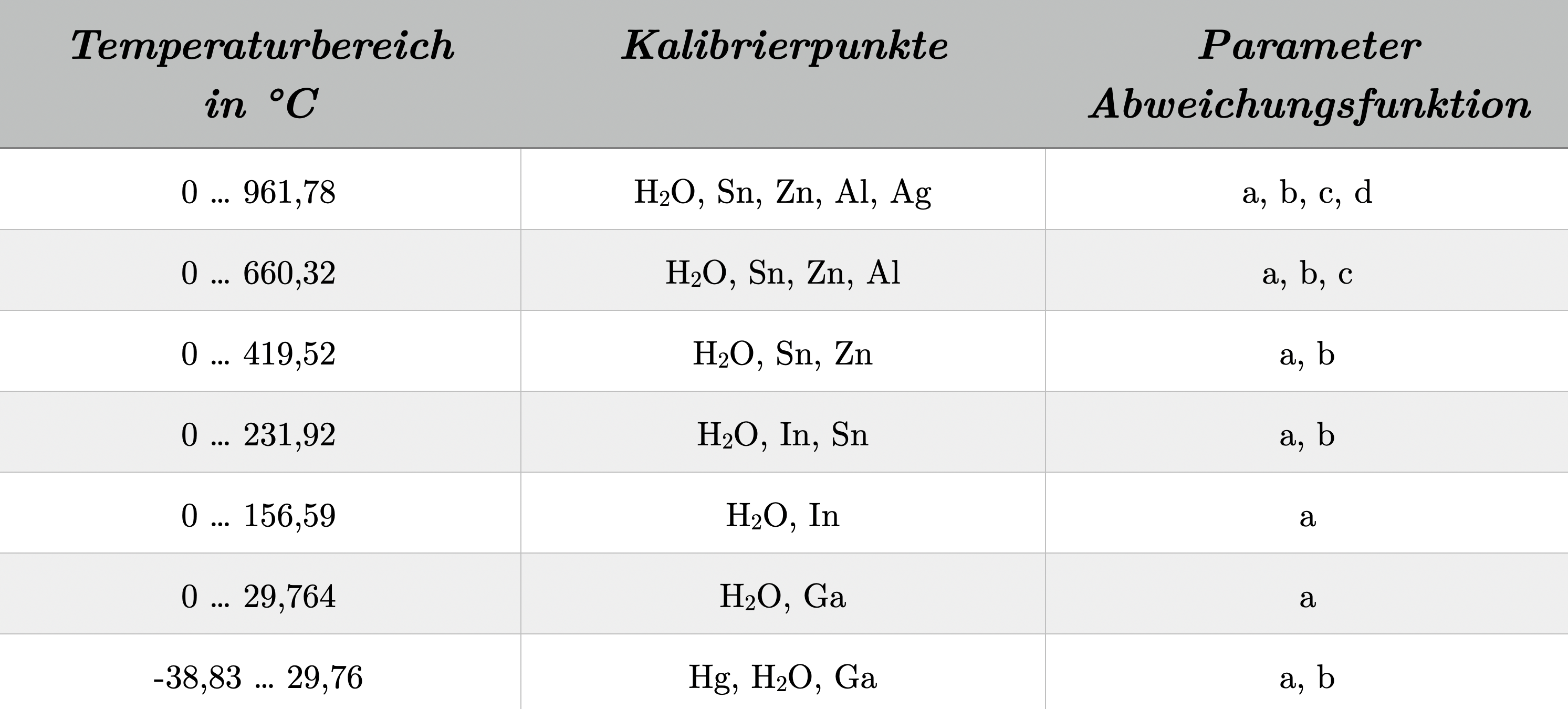
The International Temperature Scale of 1990 (ITS-90) not only establishes the defining temperature fixed points with the corresponding temperatures at which thermometers are calibrated but also the corresponding calibration ranges.

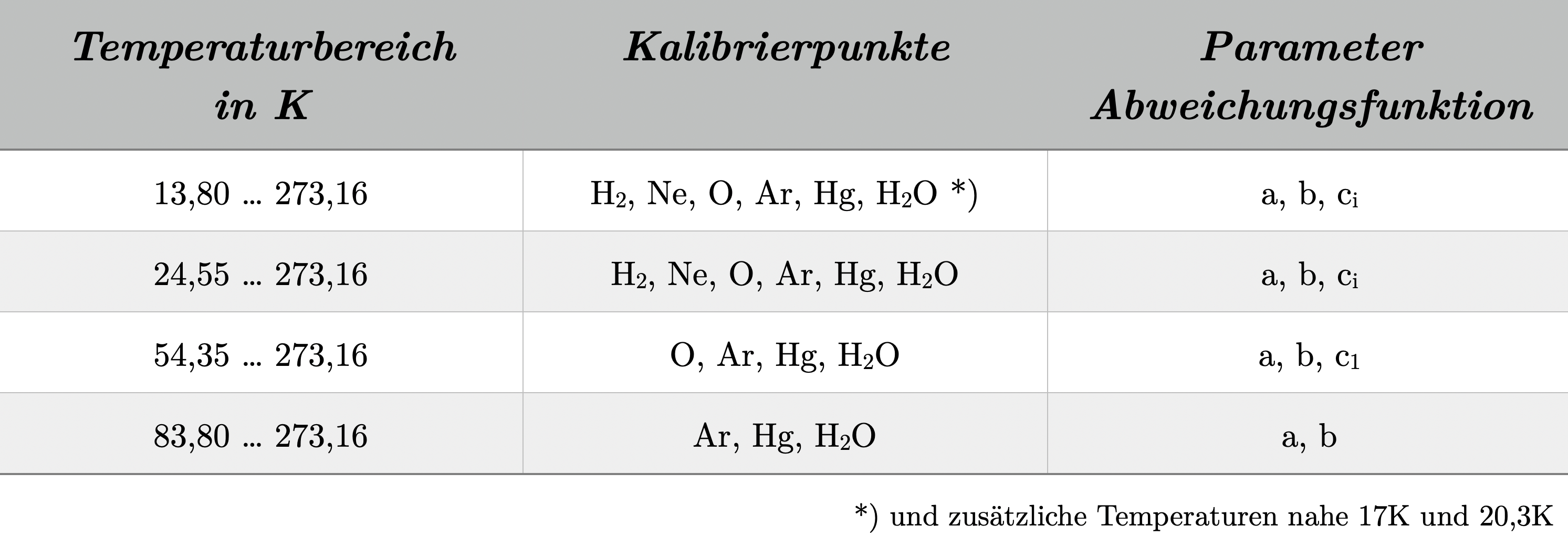
By definition, there are two ranges: one for the negative temperature range, which starts at approximately 13 K and extends to the water triple point at 0.01 °C, and one for the positive temperature range. The latter starts at the water triple point at 0.01 °C (or in the range from the mercury triple point at -38.8344 °C to the gallium melting point at 29.7646 °C) and extends to the silver freezing point at 961.78 °C.

Depending on the temperature range, the parameters for the ITS-90 deviation function are defined. In the range from the argon triple point to the freezing point of silver, the parameters a, b, c, and d are used. This temperature range is also the practical range used in calibration laboratories for calibrating thermometers. In extreme ranges at very low temperatures, such as the oxygen triple point, there is an additional parameter ci, which is only used at these extreme temperatures.

The graphic provides a visual representation of the corresponding defining ITS-90 temperatures at the temperature fixed points and their associated temperatures. For example, the temperature of the aluminum freezing point is 660.323 °C.

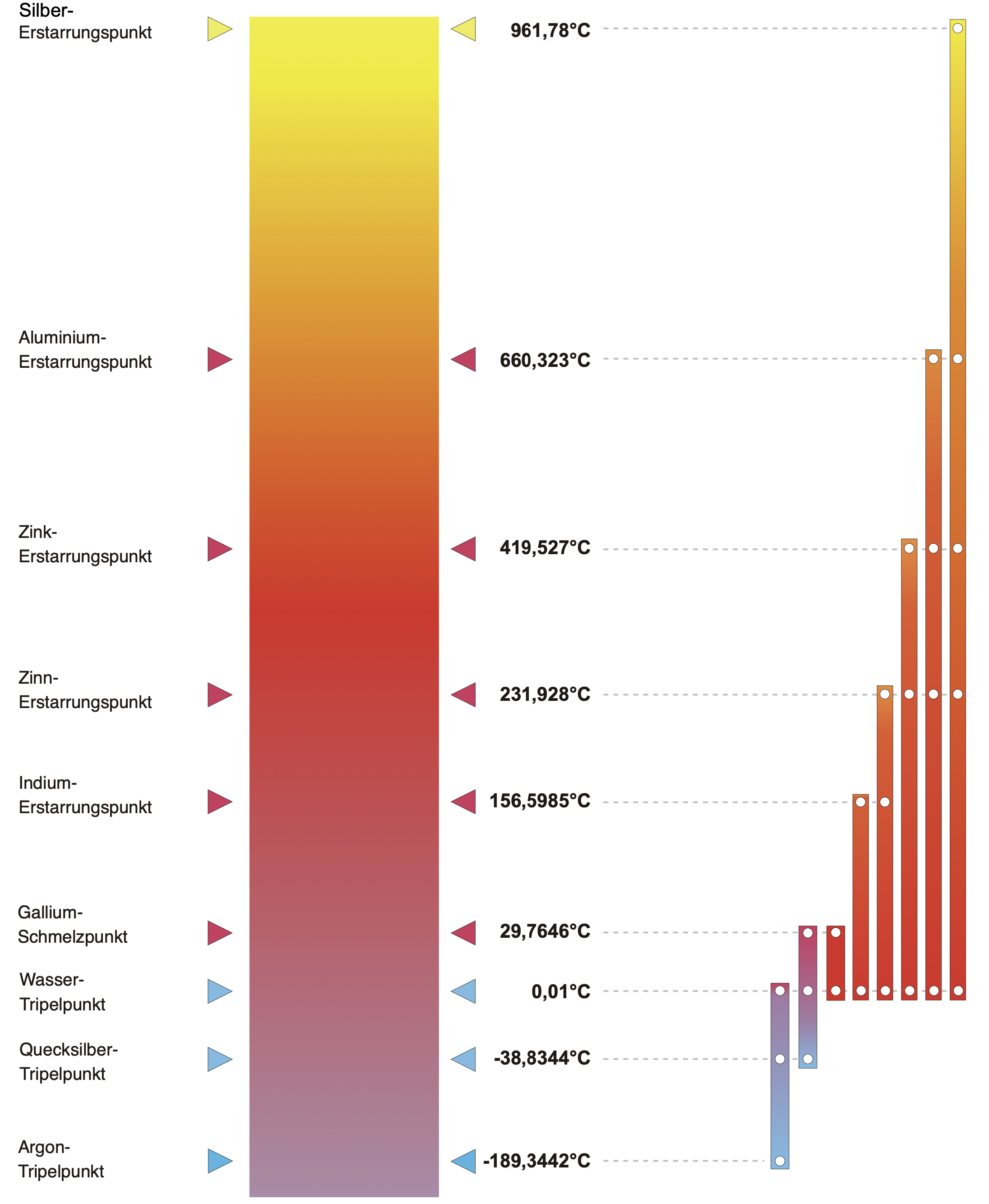
It is important to know that with thermometers calibrated at the ITS-90 temperature fixed points, one must only interpolate and not extrapolate.

This means, for instance, if a temperature of about 500 °C is to be measured, then the highest calibration point must be the aluminum freezing point at 660.323 °C and not the zinc freezing point at 419.527 °C. Because at 419 °C, one would have to extrapolate up to 500 °C. Therefore, the range is always chosen so that the temperature to be measured can be calculated by interpolation.

The corresponding calibration ranges are schematically shown in the graphic. In our example, this would mean that if we want to measure at 500 °C, we would use the calibration range up to the aluminum freezing point at 660.323 °C and accordingly would need to calibrate at aluminum, zinc, tin, and the water triple point. This would be the second calibration range from the right in the representation.

The white points represent the necessary temperature fixed points for calibration. The temperature fixed points at the freezing of indium and at the gallium melting point would therefore not be necessary. They do not factor into the calibration and the subsequent calculation of the characteristic curve – i.e., the deviation function and the reference function of the International Temperature Scale of 1990 (ITS-90).

Applying the ITS-90 in Everyday Practice

The International Temperature Scale of 1990 (ITS-90) is applied almost daily in the routine of a temperature calibration laboratory. Often, users are not aware of this fact, as the mathematics of the ITS-90 are embedded in the temperature measuring devices and measuring bridges and run in the background.

It’s important to understand that temperature cannot be measured directly, but is calculated, for example, through the resistance of a material. The ITS-90 contains the mathematical foundations for calculating temperatures from resistance measurements of standard thermometers (SPRT) of the ITS-90.

A frequently asked question is how the ITS-90 can be meaningfully used as a characteristic curve in the daily work of a laboratory.

Therefore, in this blog post, I will show through an example how the corresponding temperature can be calculated from measured resistances using the ITS-90. In my seminars, I like to explain this example in detail.

The ITS-90 uses so-called W-values, which represent the ratio of the measured resistance to the last known value of the water triple point. Using this calculated W-value and the reference and deviation functions derived from the ITS-90, temperatures can be determined. The calculation of the W-value is done according to the following formula:

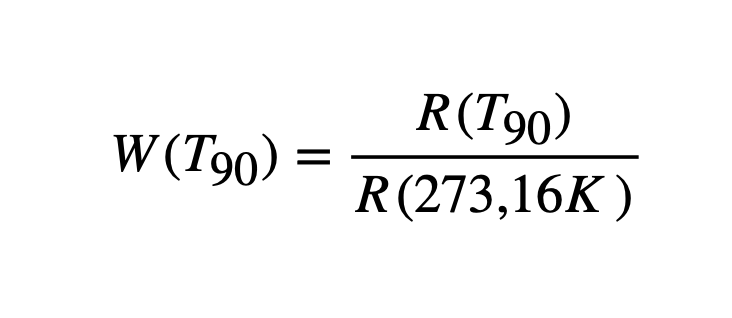
Here, R(T90) represents the measured resistance at temperature T90, and R(273.16 K) stands for the resistance at the water triple point (more precisely at 273.16 Kelvin).

In the next calculation step, the reference functions (10a and 10b) and the deviation function (14) are needed, which were defined according to the ITS-90 (International Temperature Scale of 1990). We only use the functions that are relevant for our temperature range.

Reference functions:

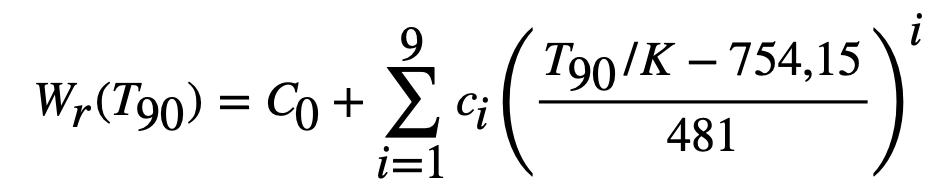
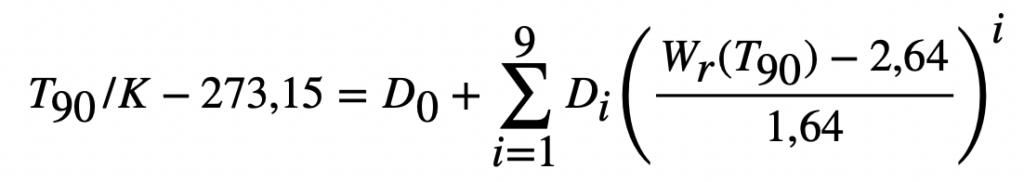
The reference function is used with the following parameters:

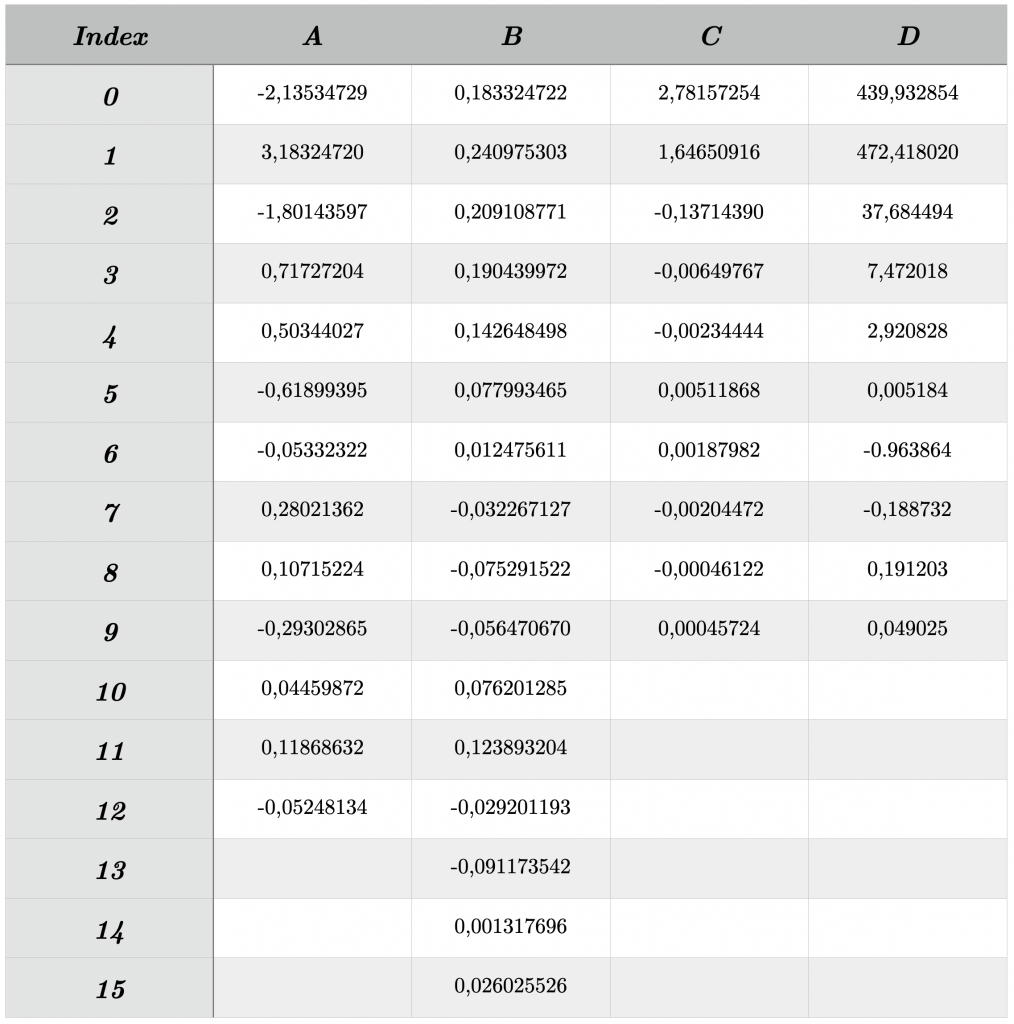
The deviation function is as follows:

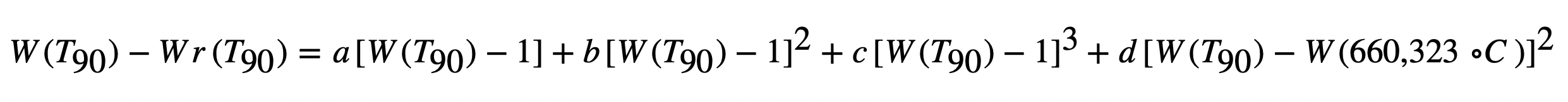
The equations and tables are taken from the ITS-90 publication by Walter Blanke (see references).

ITS-90 Calculation Example

Let’s assume you measure a resistance value of 31.1428 Ohm. From the calibration certificate, you obtain the following information:

R(0.01°C) = 25.1648 Ohm

a = -1.6093e-03
b = 1.9911e-03

First, you calculate the W-value:

W(t90) = R(t90) / R(0.01°C)
W(t90) = 31.1428 Ohm / 25.1648 Ohm
W(t90) = 1.23755404

With the deviation function (14), you can then calculate the Wr(t90) value:

Wr(t90) = 1.237824

With the determined value, you can now calculate the temperature t90 using the reference function (10b):

t90 = 60.1873°C

In this way, the corresponding temperature can be calculated from the measured resistance value.

References for ITS-90

The International Temperature Scale of 1990 (ITS-90) can be obtained from several sources:

1. The original German document: Blanke, Walter. Die Internationale Temperaturskala von 1990: ITS-90. Physikalisch-Technische Bundesanstalt, Wirtschaftsverlag NW, Verlag für Neue Wissenschaft, Braunschweig, 1989. [ISBN 3-89429-040-4].
2. A digital version of the original document is available from the National Institute of Standards and Technology (NIST). You can find the document here.
3. PTB website: The implementation of ITS-90 in Germany and further information can be found on the website of the Physikalisch-Technische Bundesanstalt (PTB). Go to the PTB website here.
4. Wikipedia: The Wikipedia article on ITS-90 provides a good overview and can be a good starting point for those new to the topic. Go to the Wikipedia article here.
5. ITS-90 website: This website offers a lot of useful information about ITS-90 and is a great resource for anyone who wants to know more about the topic. Go to the ITS-90 website here.

Sources:

• Walter Blanke: Die Internationale Temperaturskala von 1990: ITS-90
• Thomas Klasmeier: Table Book “Temperature”, Edition 3