Termometry rezystancyjne: zasada działania i zastosowanie

Termometry rezystancyjne Pt100 to precyzyjne czujniki temperatury, szeroko stosowane w wielu zastosowaniach przemysłowych i naukowych. Ich zasada działania opiera się na zmianie rezystancji elektrycznej drutu platynowego w zależności od temperatury. „Pt” w Pt100 oznacza platynę, materiał, z którego wykonany jest drut, a „100” oznacza, że rezystancja w 0°C wynosi dokładnie 100 omów.

Termometry rezystancyjne Pt100 oferują szeroki zakres temperatur, od -200°C do +850°C, i charakteryzują się wysoką dokładnością. Ich krzywa rezystancji w funkcji temperatury jest niemal liniowa, co ułatwia kalibrację i interpretację zmierzonych wartości.

Czujniki te zmieniają swoją rezystancję elektryczną proporcjonalnie do zmiany temperatury. Współczynnik temperaturowy wynosi około 0,385 oma/°C przy 0°C. Czujniki Pt100 mają zwykle dwa, trzy lub cztery złącza. W związku z tym mogą być stosowane w różnych konfiguracjach obwodów, w tym w układach 2-przewodowych, 3-przewodowych i 4-przewodowych.

Aby zapewnić dokładne pomiary, termometry rezystancyjne Pt100 muszą być chronione przed wpływami zewnętrznymi, takimi jak wilgoć i obciążenia mechaniczne. Często odbywa się to poprzez zastosowanie rur ochronnych. Dodatkowo, powinny być regularnie kalibrowane, albo w specjalistycznych laboratoriach, albo za pomocą termometrów referencyjnych.

Czujniki Pt100 znajdują zastosowanie w wielu dziedzinach, w tym w przemyśle spożywczym, laboratoriach, technice klimatyzacyjnej, przemyśle motoryzacyjnym i chemicznej inżynierii procesowej.

Jak działają termometry rezystancyjne?

Termometry rezystancyjne są często używane do precyzyjnych pomiarów temperatury. Typowy zakres temperatur wynosi od około -50 °C do 600 °C, chociaż istnieją specjalne zastosowania, w których termometry rezystancyjne są używane od -200 °C do ponad 1000 °C. Przedstawiony termometr rezystancyjny Pt100 pochodzi z laboratorium kalibracyjnego firmy Klasmeier.

Zasada pomiaru tych termometrów opiera się na pomiarze rezystancji elektrycznej rezystorów pomiarowych, dla których podstawowe jest prawo Ohma:

U = R ⋅ I = stała

gdzie:
U = napięcie,
R = rezystancja,
I = prąd

W szkole prawo Ohma jest często przedstawiane jako trójkąt, który ilustruje związek między prądem, napięciem i rezystancją.

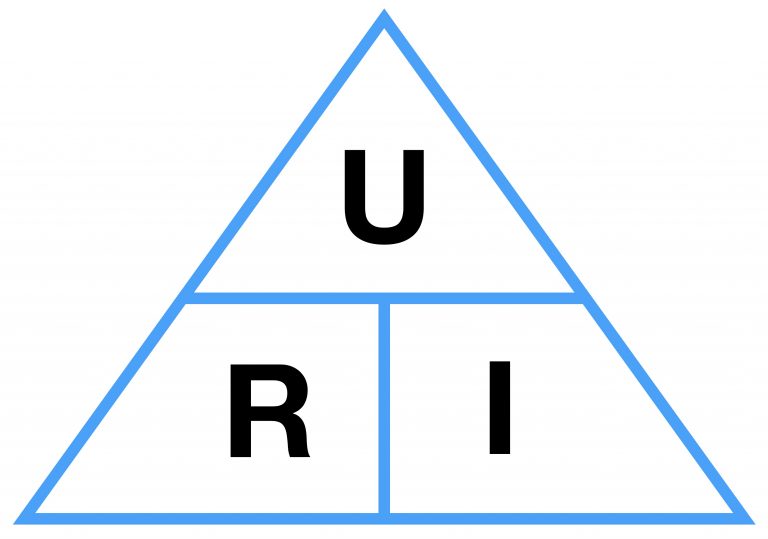
Jeśli znane są dwie z tych wielkości, można obliczyć trzecią. Na schemacie obwodu prawo Ohma jest przedstawione jak na poniższym rysunku.

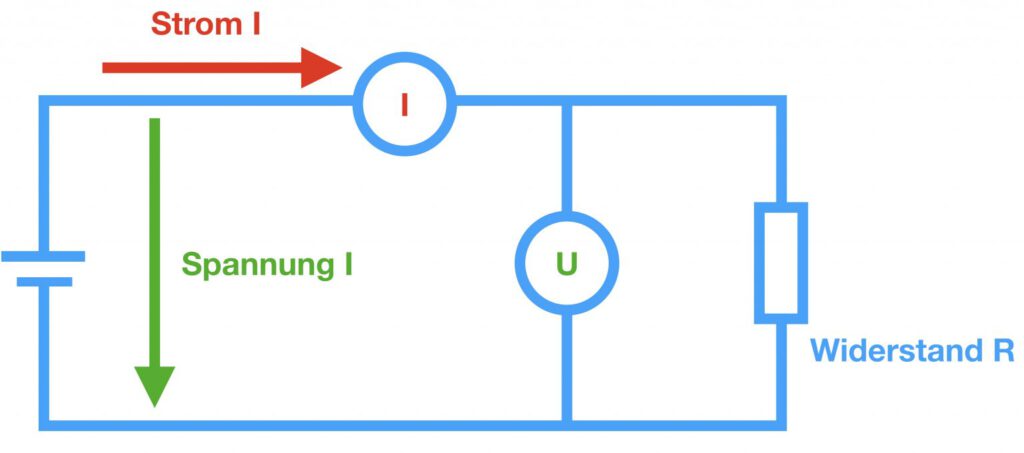
Zależności pomiaru rezystancji, a tym samym termometru rezystancyjnego, można również przedstawić graficznie na schemacie.

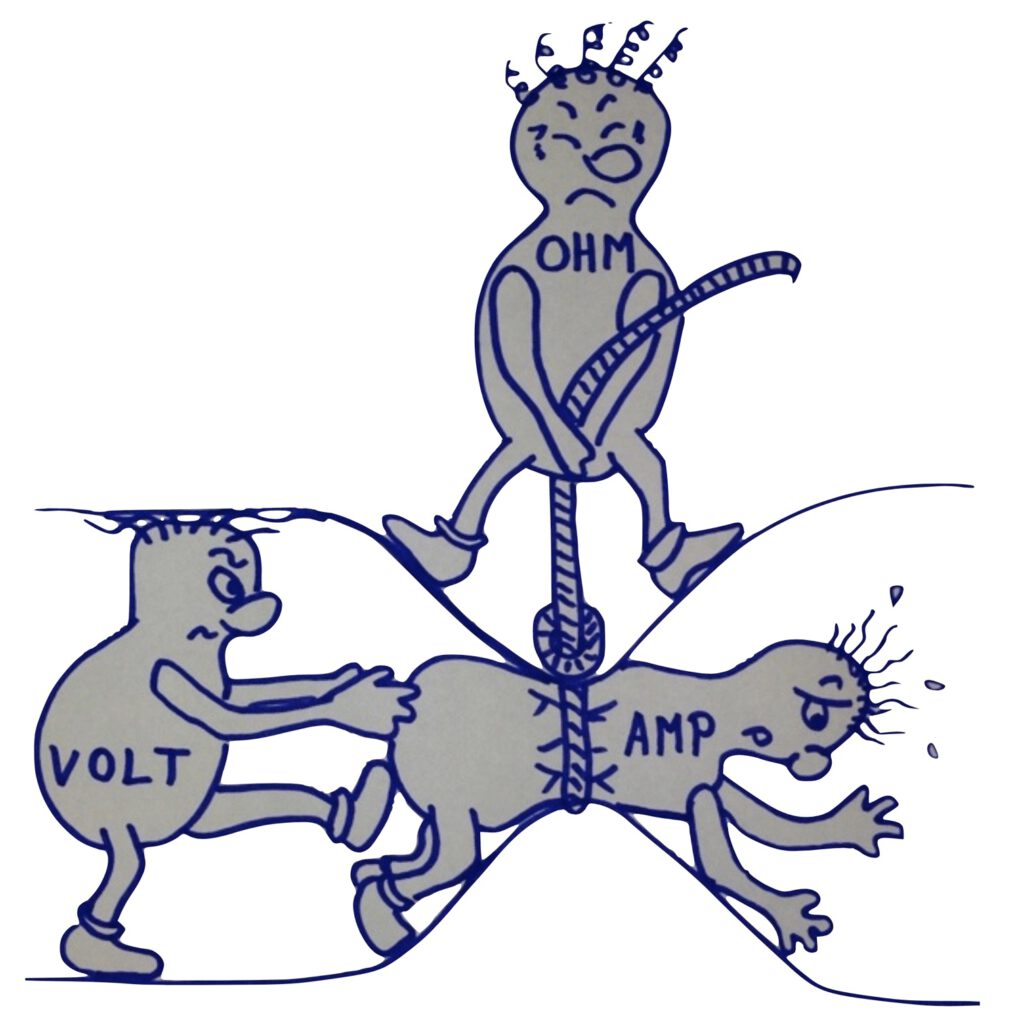
W tym przypadku „VOLT-ludzik” (U – napięcie) jest przepychany przez „AMP-ludzika” (I – prąd) przez rurę, podczas gdy „OHM-ludzik” (R – rezystancja) próbuje temu zapobiec, zwężając rurę. Sukces „OHM-ludzika” zależy od temperatury: im jest cieplej, tym trudniej „VOLT-ludzikowi” poruszyć „AMP-ludzika”. Ponieważ ten zależny od temperatury efekt jest powtarzalny, zasada pomiaru rezystancji elektrycznej może być wykorzystana do pomiaru temperatury. Zmierzona rezystancja R w omach jest przeliczana na temperaturę T w °C lub K za pomocą znanego związku.

Zasadniczo każdy przewodnik elektryczny, dla którego obowiązuje prawo Ohma, może być używany jako termometr. Rezystywność jest stałą fizyczną, która opisuje tę właściwość. Przegląd w pokazuje różne rezystywności materiałów w temperaturze 20 °C.

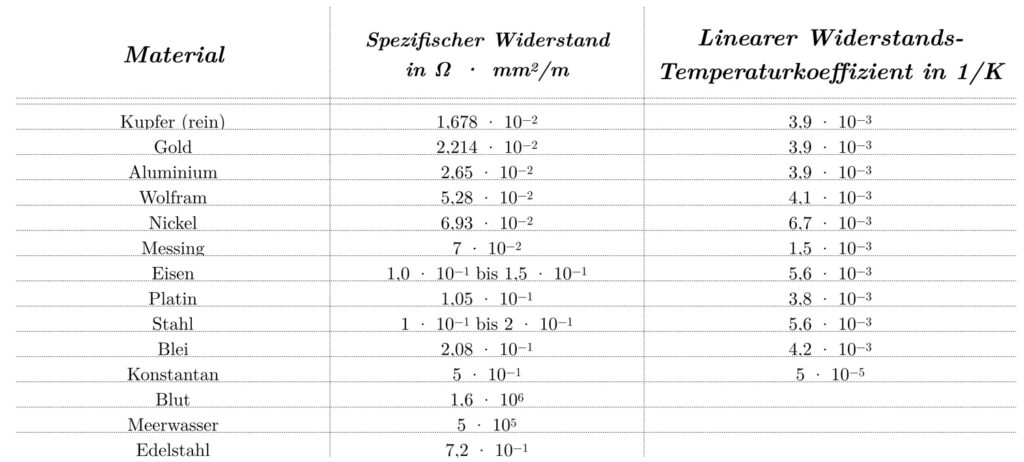
Chociaż wszystkie wymienione materiały mogą być zasadniczo używane do pomiaru temperatury, istnieją pewne kryteria wyboru materiału do produkcji termometrów. Materiał powinien mieć wysoką rezystywność i zasadniczo nadawać się do tego celu. Na przykład ludzka krew ma doskonałą rezystywność wynoszącą 1,6×106 Ω⋅mm2 /m, ale nie nadaje się do przemysłowej produkcji termometrów. Metale są bardziej odpowiednie do tego celu.

Oprócz rezystywności ważny jest również liniowy współczynnik temperaturowy rezystancji. Opisuje on zmianę rezystancji materiału na stopień Celsjusza i jest podawany w 1/K. Może być również określany jako czułość. Aby zminimalizować wymagania dotyczące techniki pomiarowej, współczynnik ten powinien być jak największy. Należy zatem znaleźć najlepszy kompromis między kosztami, zasadniczą przydatnością materiału, rezystywnością i współczynnikiem temperaturowym rezystancji.

Nikiel i platyna okazały się odpowiednimi materiałami. Początkowo rezystory niklowe, takie jak Ni100, były uważane za faworytów, ponieważ wykazywały wyższą czułość niż rezystory platynowe. Wykazywały jednak większe odchylenia graniczne i ograniczony zakres temperatur. Norma dla termometrów niklowych, DIN 43760, została wycofana w latach 90. Od tego czasu rezystory niklowe są używane głównie w specjalnych zastosowaniach technicznych.

Z biegiem czasu rezystory platynowe, takie jak Pt100, zyskały na popularności. Są one szeroko stosowane w przemysłowej technice pomiarowej i stanowią obecnie standard elektrycznego pomiaru temperatury za pomocą termometrów rezystancyjnych.

Charakterystyka Pt100 dla termometrów rezystancyjnych – proste wyjaśnienie

Czujniki platynowe ugruntowały swoją pozycję jako termometry rezystancyjne. Związek między temperaturą a rezystancją w termometrach platynowych jest opisywany nie proporcjonalnie, ale za pomocą wielomianu wyższego rzędu:

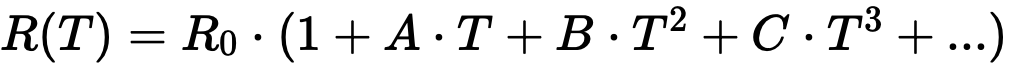
Gdzie:

R(T) = rezystancja termometru
R0 = rezystancja termometru w 0 °C
A, B, C, … = indywidualne parametry termometru lub norma
T = temperatura

Równanie Callendara-Van Dusena

Równanie Callendara-Van Dusena to wzór używany do opisania zależności między temperaturą a rezystancją elektryczną platynowego czujnika temperatury rezystancyjnego.

Równanie Callendara-Van Dusena jest również skracane jako „CVD” i jest stosowane od lat 20. XX wieku. Charakterystyka jest znormalizowana w normie DIN EN 60751, która opisuje przemysłowe platynowe termometry rezystancyjne i platynowe czujniki temperatury. Została opublikowana po raz pierwszy w latach 90. i w swojej ostatniej wersji jako DIN EN 60751:2009-05 jest nadal ważna.

Samo równanie Callendara-Van Dusena można sformułować w dwóch częściach, dla temperatur powyżej i poniżej 0 °C:

Dla temperatur T > 0 °C:

Dla temperatur T 0 °C:

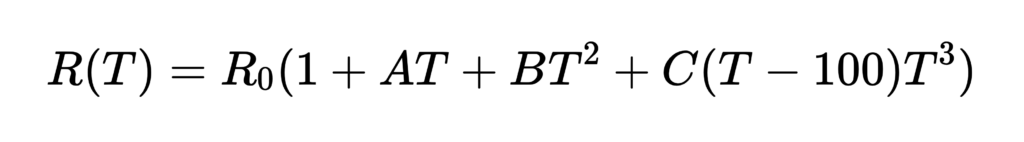
Gdzie:

• R(T) rezystancja w temperaturze ( T )
• R0 rezystancja w 0 °C
• A, B i C to współczynniki zależne od platynowego termometru rezystancyjnego

W normie DIN EN 60751:2009-05 współczynniki dla równania Callendara-Van Dusena są znormalizowane:

A=3,9083×10 −3 °C-1
B=−5,775×10 −7 °C-2
C=−4,183×10 −12 °C-4

Możliwe jest jednak również kalibrowanie poszczególnych termometrów i obliczanie indywidualnych współczynników. Ma to tę zaletę, że termometr nie musi być już oceniany na podstawie odchyleń granicznych normy, ale może być indywidualnie dopasowany do własnej charakterystyki.

Równanie Callendara-Van Dusena umożliwia przeprowadzanie bardzo precyzyjnych pomiarów temperatury poprzez wstawienie zmierzonej rezystancji termometru do równania Callendara-Van Dusena i obliczenie temperatury.

Poniższy rysunek przedstawia dwa zakresy temperatur równania Callendara-Van Dusena. Na niebiesko przedstawiony jest zakres temperatur od -200 °C do 0 °C, a na czerwono zakres temperatur od 0 °C do 850 °C.

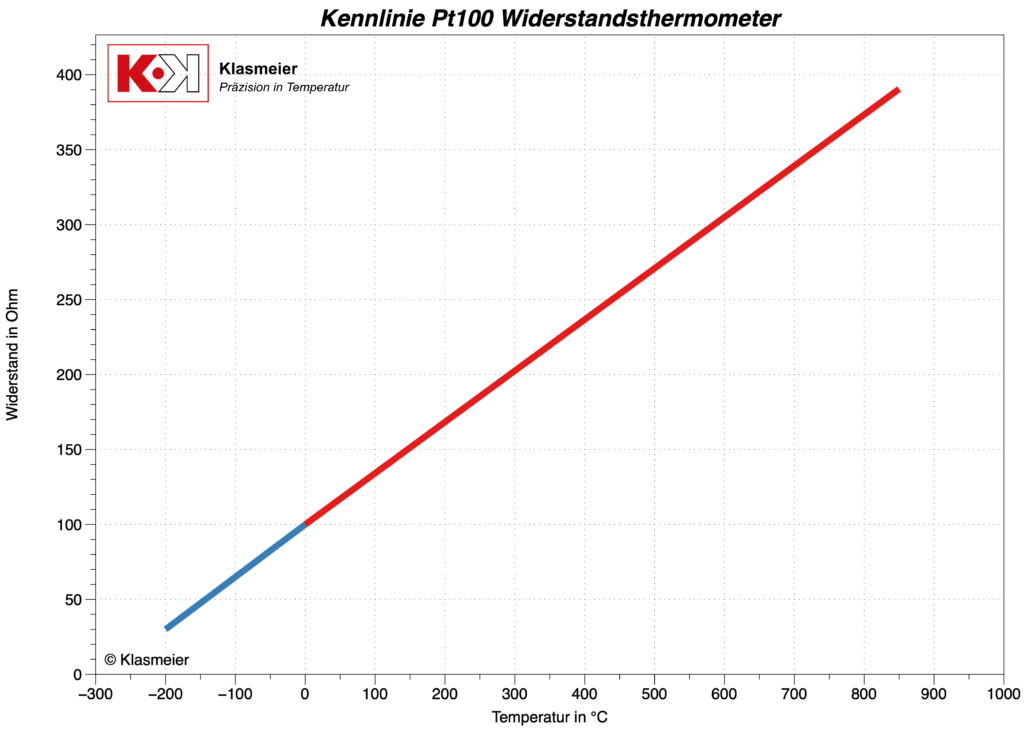
Rezystancja nominalna R0 termometrów rezystancyjnych

Aby lepiej sklasyfikować rezystory pomiarowe, w normie DIN EN 60751 wprowadzono tak zwaną rezystancję nominalną R0. Opisuje ona rezystancję elektryczną czujnika temperatury w temperaturze 0 °C. Na przykład czujnik temperatury Pt100 ma rezystancję 100 omów w temperaturze 0 °C. W normie wymienione są następujące rezystancje nominalne:

• Pt 10 = 10 omów przy 0 °C
• Pt 100 = 100 omów przy 0 °C
• Pt 500 = 500 omów przy 0 °C
• Pt 1.000 = 1.000 omów przy 0 °C

Odmienne rezystancje nominalne, takie jak Pt 25, Pt 2,5 lub Pt 0,25, są stosowane w termometrach precyzyjnych i często spełniają wymagania ITS-90. Są one wówczas określane jako SPRT lub termometry wzorcowe. W zastosowaniach laboratoryjnych często preferowane są termometry Pt 25, ponieważ oferują dobry kompromis między stabilnością, czułością i samonagrzewaniem.

Współczynnik temperaturowy w termometrach rezystancyjnych

Różnica między termometrami znormalizowanymi a termometrami wzorcowymi zgodnie z ITS-90 uwidacznia się w tak zwanym współczynniku temperaturowym, który w normie jest definiowany przez pomiar rezystancji w temperaturze 0 °C i 100 °C:

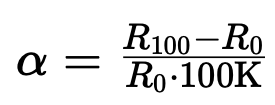
Gdzie:

alfa = wzrost termometru w 1/K
R100 = rezystancja w 100 °C w omach
R0 = rezystancja w 0 °C w omach

Wartość alfa przemysłowych czujników temperatury zgodnie z normą wynosi 3,85 10^-3/K, podczas gdy wartość alfa termometrów wzorcowych zgodnie z ITS-90 wynosi 3,92875 10^-3/K. Wartość ta odpowiada czułości spektralnie czystej platyny w tym zakresie temperatur.

Czułość w termometrach rezystancyjnych

Czułość termometru rezystancyjnego opisuje, jak bardzo zmienia się rezystancja czujnika w odniesieniu do zmiany temperatury. Jest to miara tego, jak dokładnie czujnik reaguje na zmiany temperatury. W przypadku Pt100 rezystancja zmienia się o około 0,385 oma na każdy stopień Celsjusza zmiany temperatury. Ta szybkość zmiany, znana jako współczynnik temperaturowy, jest bezpośrednią miarą czułości czujnika. Czułość ma kluczowe znaczenie dla dokładności i rozdzielczości czujnika. Czujnik o wyższej czułości może wykrywać mniejsze zmiany temperatury i umożliwia dokładniejsze pomiary temperatury. Jest to szczególnie ważne w zastosowaniach, w których wymagana jest precyzyjna kontrola temperatury, takich jak laboratoria lub sterowanie procesami w przemyśle.

Należy jednak również pamiętać, że czujniki temperatury o dużej czułości często charakteryzują się wysokim samonagrzewaniem i mniejszą stabilnością długoterminową. Dlatego należy bardzo rozważnie dobierać stosunek między wartością nominalną a czułością czujnika temperatury.

Aby osiągnąć zdefiniowaną rezystancję nominalną, dostosowuje się długość lub średnicę drutu platynowego w rezystorze pomiarowym. Powoduje to zmianę nie tylko rezystancji, ale także czułości czujników na około:

• Pt 10 = 0,04 oma / K
• Pt 100 = 0,4 oma / K
• Pt 500 = 2 oma / K
• Pt 1.000 = 4 oma / K

Technologie podłączania termometrów rezystancyjnych

Termometry rezystancyjne można podłączać do urządzeń pomiarowych, rejestratorów danych lub mostków pomiarowych, a do tego celu dostępne są różne techniki.

• Technika dwuprzewodowa
• Technika trzyprzewodowa
• Technika czteroprzewodowa

Technika dwuprzewodowa

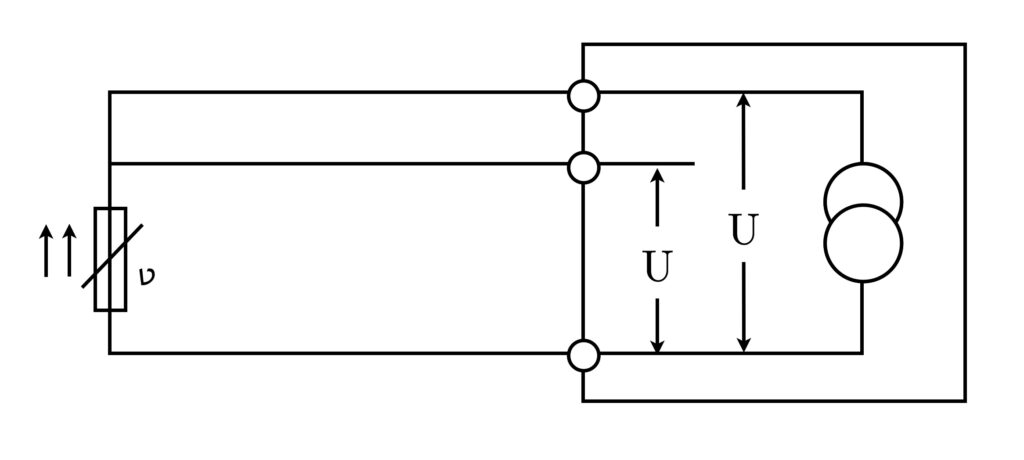
Technika dwuprzewodowa pokazuje, jak podłączyć czujnik temperatury do urządzenia pomiarowego, jak widać na rysunku. Ważne jest, aby uwzględnić rezystancję kabli połączeniowych, ponieważ są one połączone szeregowo z rezystorem pomiarowym.

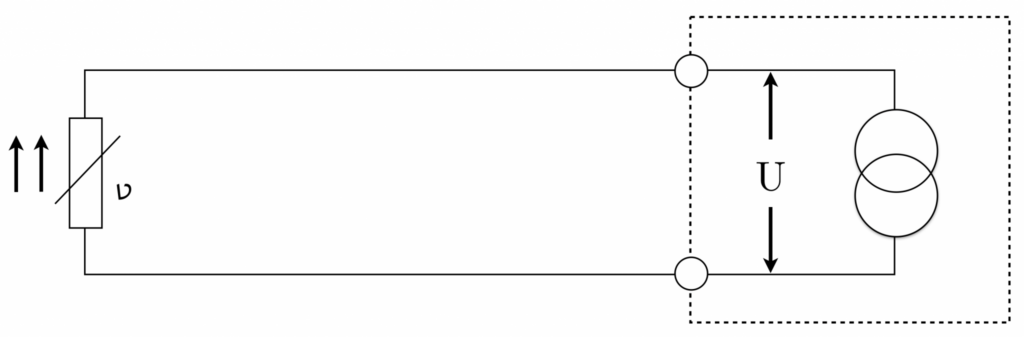
Wynikowy pomiar jest sumą rezystancji przewodu 1, rezystora pomiarowego (właściwego czujnika temperatury) i przewodu 2, co prowadzi do zwiększonego pomiaru. Dlatego korekta wyniku pomiaru jest niezbędna do wyeliminowania błędów pomiarowych.

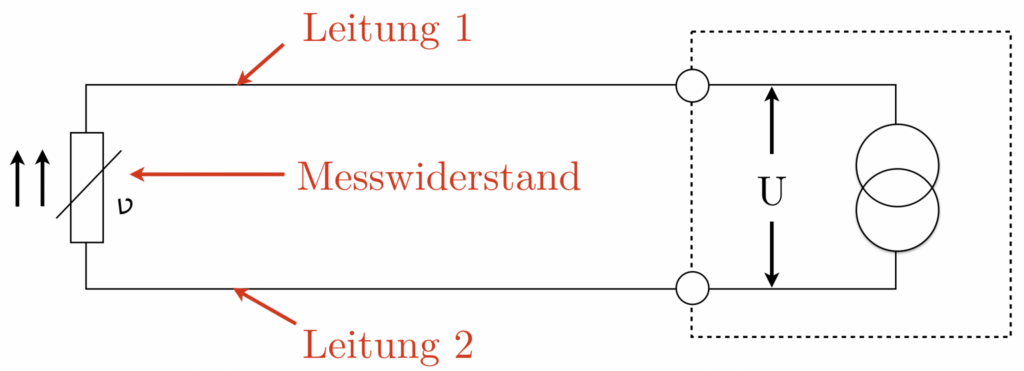
Przykładowy przykład obliczeniowy demonstruje zakres odchylenia pomiarowego w określonych warunkach zastosowania. Załóżmy, że czujnik temperatury jest podłączony za pomocą przewodu miedzianego, w następujących określonych warunkach:

• Rezystywność przewodu miedzianego w temperaturze pokojowej: 0,017
• Przekrój przewodu: 0,5 mm^2
• Długość przewodu: ok. 50 m

Odchylenie pomiarowe spowodowane przewodem przyłączeniowym można obliczyć za pomocą równania

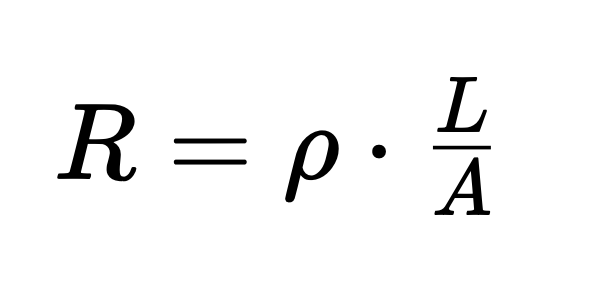
gdzie:

• R to rezystancja przewodu,
• ho to rezystywność,
• L to długość przewodu i
• A reprezentuje powierzchnię przekroju.

W tym kontekście rezystancja przewodu wynosi 3,4 oma:

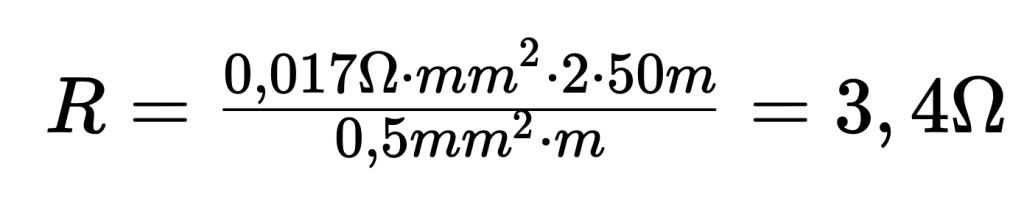
Biorąc pod uwagę czułość ( E ) czujnika temperatury PT 100 wynoszącą około 0,385 oma / K, odchylenie pomiarowe wynosi 8,8 K.

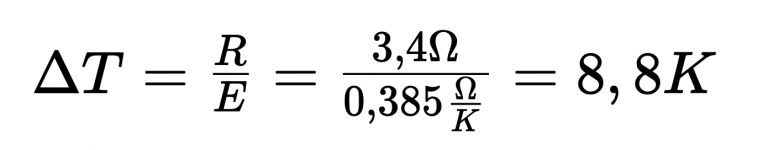
Długość przewodu wynosząca około 50 m musi być uwzględniona dwukrotnie, zarówno dla „drogi do” (przewód 1), jak i dla „drogi powrotnej” (przewód 2).

Z historycznego punktu widzenia było całkiem konwencjonalne podłączanie termometrów w zakładach produkcyjnych za pomocą techniki dwuprzewodowej. Przed erą technologii cyfrowej, która uprościła korektę błędów systematycznych, stosowano tabele korekcyjne w celu uzyskania dokładnych odczytów.

Przykład ilustruje wartości korekcyjne przewodu przyłączeniowego o długości 10 m w zależności od przekroju przewodu.

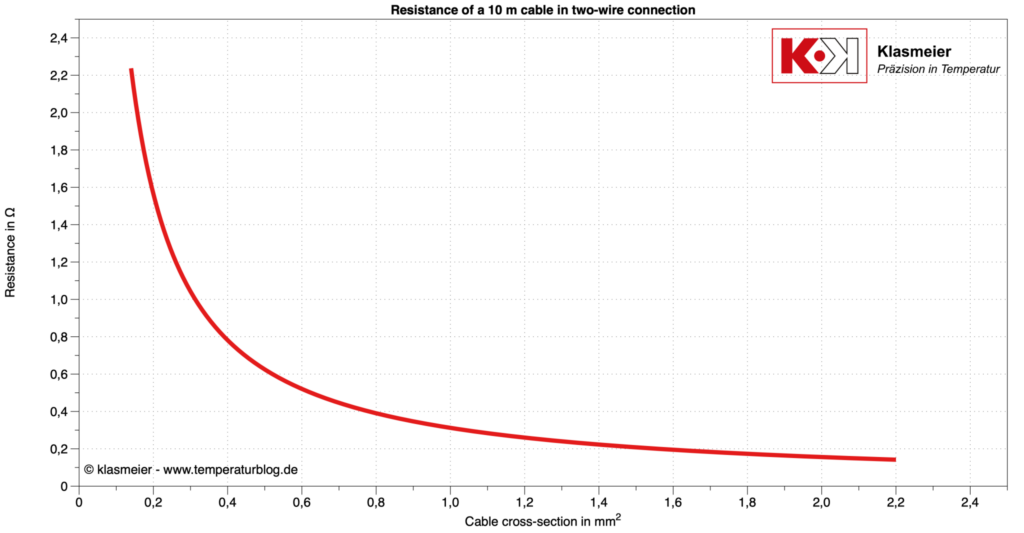
W przypadku przewodu przyłączeniowego o przekroju 0,5 mm^2 rezystancja w obwodzie dwuprzewodowym o długości 10 m wynosi 0,6 oma. Oznacza to, że odczyty należy skorygować o ten współczynnik. W przypadku Pt100 odpowiada to około 1,6 °C.

Na poniższym rysunku przedstawiono wartości korekcyjne dla Pt100 w odniesieniu do przekroju przewodu miedzianego o długości 10 m w technice dwuprzewodowej.

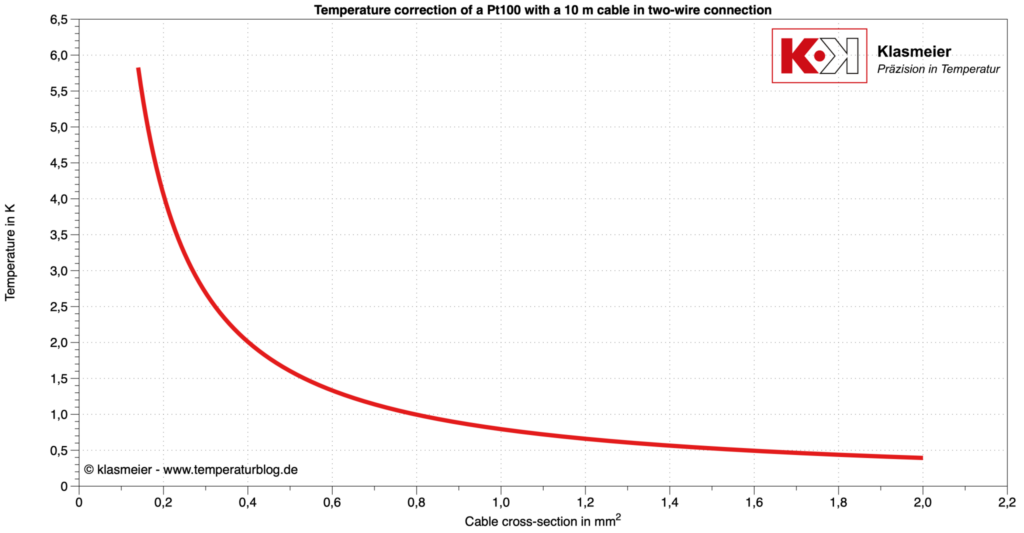
Technika trzyprzewodowa

Technika trzyprzewodowa stanowi optymalizację w stosunku do techniki dwuprzewodowej, szczególnie w odniesieniu do minimalizacji błędów pomiarowych spowodowanych rezystancją przewodów. W tej konfiguracji stosuje się trzy przewody, przy czym dwa przewody są połączone równolegle do rezystora pomiarowego, a trzeci przewód służy do kompensacji rezystancji przewodu.

Kompensacja rezystancji przewodu odbywa się za pomocą mostka pomiarowego, który uwzględnia rezystancję trzeciego przewodu i tym samym odejmuje całkowitą rezystancję przewodów przyłączeniowych. Skutkuje to dokładniejszym pomiarem właściwej rezystancji pomiarowej, ponieważ minimalizowane są wpływy przewodów przyłączeniowych.

Chociaż technika trzyprzewodowa stanowi znaczną poprawę w stosunku do techniki dwuprzewodowej, jest nadal podatna na błędy spowodowane zmianami temperatury i różnymi długościami przewodów, które mogą wpływać na kompensację rezystancji przewodu.

Technika czteroprzewodowa

Technika czteroprzewodowa, znana również jako pomiar Kelvina czteroprzewodowy, stanowi dalszą optymalizację w precyzji pomiaru rezystancji, szczególnie w zastosowaniach, w których wymagana jest najwyższa dokładność. Technika ta wykorzystuje dwa dodatkowe przewody do dostarczania prądu pomiarowego i pomiaru spadku napięcia na czujniku, eliminując w ten sposób wpływ rezystancji przewodu.

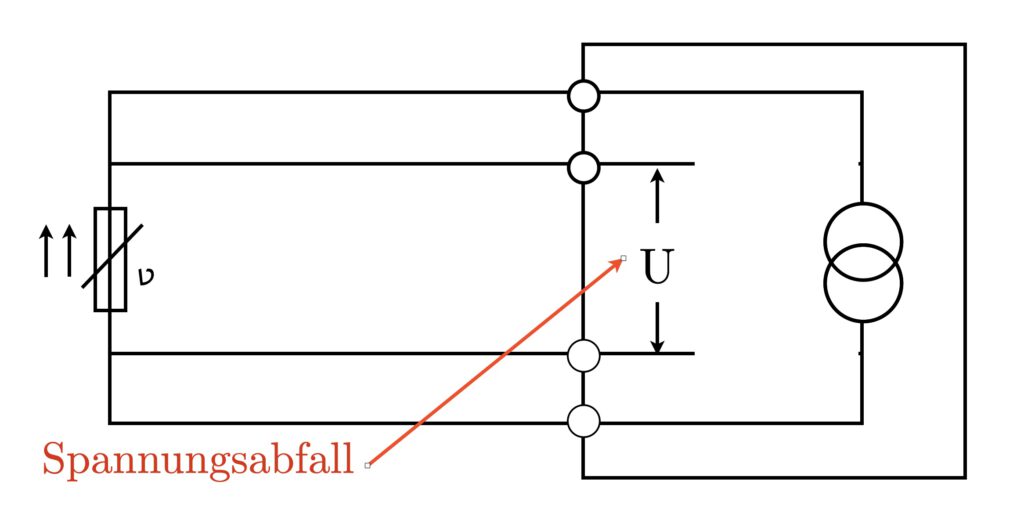
W tej konfiguracji prąd pomiarowy przepływa przez dwa przewody (przewody prądowe), podczas gdy pozostałe dwa przewody (przewody napięciowe) służą do pomiaru spadku napięcia bezpośrednio na czujniku. Ponieważ prąd pomiarowy nie przepływa przez przewody napięciowe, rezystancja tych przewodów nie jest uwzględniana w pomiarze, co prowadzi do większej dokładności pomiaru.

Technika czteroprzewodowa jest szczególnie korzystna w zastosowaniach z niskimi wartościami rezystancji i długimi przewodami, ponieważ umożliwia precyzyjny pomiar, który jest wolny od wpływu rezystancji przewodów.

Podsumowując, techniki trzy- i czteroprzewodowe oferują większą dokładność i niezawodność w porównaniu z techniką dwuprzewodową, minimalizując lub eliminując wpływ rezystancji przewodów. Wybór odpowiedniej techniki zależy od specyficznych wymagań aplikacji, takich jak dokładność pomiaru, warunki otoczenia i względy ekonomiczne.

Źródła

• Frank Bernhard: Handbuch der Technischen Temperaturmessung, 2. Auflage
• Thomas Klasmeier: Tablice „Temperatura”, wydanie 3
• Przemysłowe termometry rezystancyjne platynowe i czujniki temperatury platynowe (IEC 60751:2022)
• Termometr punktu miedzi ISOTECH nr 108462 do prawie 1100°C.
• Rezystywność właściwa
• DIN 43760
• Prawo Ohma